Содержание
Теорема
В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны.
Доказательство
Докажем, что если в четырёхугольник можно вписать окружность, то суммы его противоположных сторон равны.
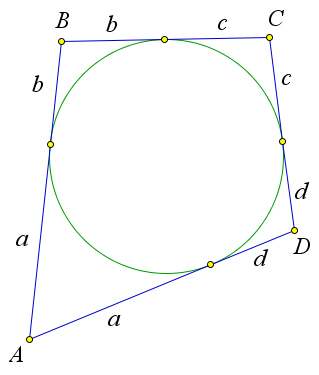
Рассмотрим произвольный четырехугольник $ABCD$, в который вписана окружность.
Вспомним, что отрезки касательных, проведенных из одной точки равны.
Обозначим равные отрезки буквами $a, b, c$ и $d$.
Тогда $AD+BC=a+d+b+c=AB+CD$.
Докажем, что если суммы противоположных сторон выпуклого четырёхугольника равны, то в него можно вписать окружность.
Пусть в выпуклом четырёхугольнике $ABCD$ выполнено равенство $AB+CD=BC+AD$.
Точка $O$ пересечения биссектрис углов $A$ и $B$ равноудалена от сторон $AD, AB$ и $BC$, поэтому можно провести окружность с центром $O$, касающуюся указанных трёх сторон.
Докажем, что эта окружность касается также стороны $CD$ и, значит, является вписанной в четырёхугольник $ABCD$.
Предположим, что это не так.
Тогда прямая $CD$ либо не имеет общих точек с окружностью, либо является секущей.
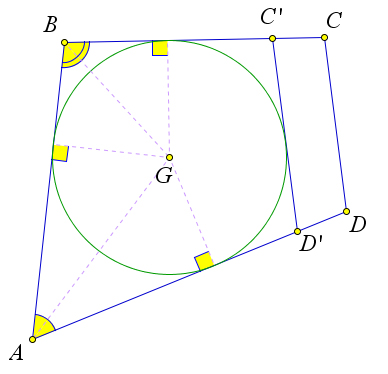
Рассмотрим первый случай.
Проведем касательную $C'D'$, параллельную стороне $CD$ ($C'$ и $D'$ – точки пересечения касательной со сторонами $BC$ и $AD$).
Так как $ABC'D'$ – описанный четырёхугольника, то $AB+C'D'=BC'+AD'$. Но $BC'=BC-CC', AD'=AD-DD'$, поэтому $C'D'+C'C+D'D=BC+AD-AB=CD$.
Таким образом $C'D'+C'C+D'D=CD$, то есть в четырёхугольнике $C'CDD'$ одна сторона равна сумме трех других сторон.
Но этого не может быть, и, значит, предположение неверно.
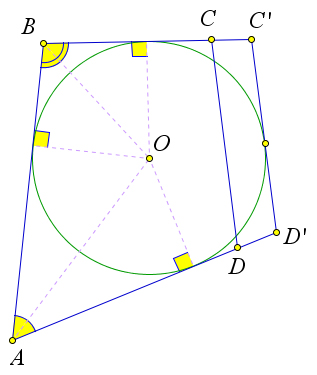
Рассмотрим второй случай.
Предположим, что прямая $CD$ является секущей окружности.
Проведем касательную $C'D'$, параллельную стороне $CD$ ($C'$ и $D'$ – точки пересечения касательной со сторонами $BC$ и $AD$).
Так как $ABC'D'$ – описанный четырёхугольника, то $AB+C'D'=BC'+AD'$.
Но $BC'=BC+CC', AD'=AD+DD'$.
Тогда $AB+C'D'=BC'+AD'=BC+CC'+AD+DD'$.
Вычитая это равенство из равенства $AB+CD=BC+AD$ получим $AB+CD-AB-C'D'=BC+AD-BC-CC'-AD-DD'$ или $C'D'=CD+CC'+DD'$.
То есть в четырёхугольнике $C'CDD'$ одна сторона равна сумме трех других сторон.
Но этого не может быть, и, значит, предположение неверно.
Следствие
В любой ромб можно вписать окружность.
Доказательство
Так как у ромба все стороны равны, то и суммы противоположных сторон равны, и, следовательно, в ромб можно вписать окружность.