Содержание
Теорема
Около четырехугольника можно описать окружность тогда и только тогда, когда сумма его противоположных углов равна $180^\circ$.
Доказательство
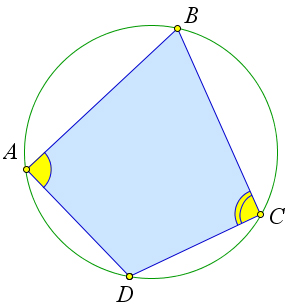
Рассмотрим произвольный вписанный четырехугольник $ABCD$.
Углы $A$ и $C$ вписанные, поэтому $\angle A=\frac{1}{2}\buildrel\,\,\frown\over{BCD}, \angle C=\frac{1}{2}\buildrel\,\,\frown\over{BAD}$.
Но так как $\buildrel\,\,\frown\over{BCD}+\buildrel\,\,\frown\over{BAD}=360^\circ$, то $\angle A+\angle C=\dfrac{1}{2}(\buildrel\,\,\frown\over{BCD}+\buildrel\,\,\frown\over{BAD})=180^\circ$.
Докажем обратное.
Пусть в произвольном четырёхугольнике $ABCD$ сумма противоположных углов равна $180^\circ$: $\angle A+\angle C=180^\circ.$
Докажем, что такой четырёхугольник можно вписать в окружность.
Заметим, что $ABCD$ – выпуклый, так как в противном случае один из его углов был бы больше $180^\circ$.
Проведём окружность через три вершины четырёхугольника: $A, B$ и $D$.
Это возможно, так как около любого треугольника можно описать окружность.
Докажем, что эта окружность проходит через вершину $C$.
Предположим, что это не так.
Тогда вершина $C$ лежит либо внутри круга, либо вне его.
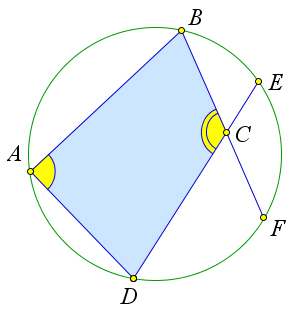
Рассмотрим первый случай.
В этом случае можно продолжить стороны $BC$ и $DC$ до пересечения с окружностью (получим соответственно точки $F$ и $E$).
Тогда $\angle C=\frac{1}{2}(\buildrel\,\,\frown\over{DAB}+\buildrel\,\,\frown\over{EF})$, и, следовательно, $\angle C>\frac{1}{2}\buildrel\,\,\frown\over{DAB}$.
Так как $\angle A=\frac{1}{2}\buildrel\,\,\frown\over{BED}$, то $\angle A+\angle C>\frac{1}{2}(\buildrel\,\,\frown\over{BED}+\buildrel\,\,\frown\over{DAB})=\frac{1}{2}\cdot360^\circ=180^\circ$.
Итак $\angle A+\angle C>180^\circ$.
Но это противоречит условию и, значит, предположение ошибочно.
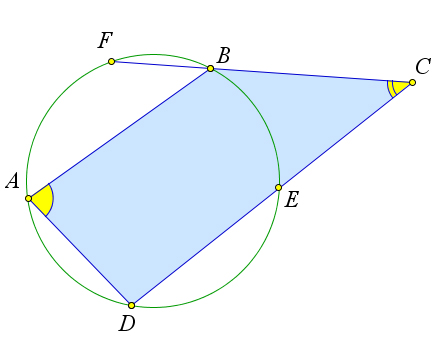
Рассмотрим второй случай.
Пусть вершина $C$ лежит вне круга.
Тогда прямые $BC$ и $CD$ являются либо секущими, либо касательными к данной окружности.
Пусть они пересекают окружность в точках $F$ и $E$ соответственно.
Пусть точка $F$ лежит на дуге $\buildrel\,\,\frown\over{AB}$, а точка $E$ на дуге $\buildrel\,\,\frown\over{BD}$ (остальные случаи расположения точек $F$ и $E$ доказываются аналогично).
В этом случае $\angle C=\frac{1}{2}(\buildrel\,\,\frown\over{BAD}-\buildrel\,\,\frown\over{BE})$, и, следовательно, $\angle C<\frac{1}{2}\buildrel\,\,\frown\over{BAD}$.
Так как $\angle A$ является вписанным, то $\angle A=\frac{1}{2}\buildrel\,\,\frown\over{BED}$.
Тогда $\angle A+\angle C<\frac{1}{2}(\buildrel\,\,\frown\over{BAD}+\buildrel\,\,\frown\over{BED})<\frac{1}{2}\cdot360^\circ=180^\circ$.
Но это противоречит условию и, значит, предположение ошибочно.
Следствие
Около трапеции можно описать окружность тогда и только тогда, когда трапеция равнобедренная.
Доказательство
Рассмотрим равнобедренную трапецию $ABCD$.
Докажем, что около неё можно описать окружность.
Действительно, так в равнобедренной трапеции $\angle A+\angle B=180^\circ, \angle B=\angle C$, следовательно, $\angle A+\angle C=180^\circ$, то есть сумма противоположных углов равнобедренной трапеции равна $180^\circ$, и, следовательно, около неё можно описать окружность.
Докажем, что если около трапеции можно описать окружность, то эта трапеция равнобедренная.
Рассмотрим трапецию $ABCD$, около которой можно описать окружность.
Тогда $\angle A+\angle C=180^\circ$.
Кроме того $\angle A+\angle B=180^\circ$.
Следовательно, $\angle C=\angle B$, и, значит, трапеция равнобедренная.