Признаки параллелограмма
- Если противоположные стороны четырехугольника попарно равны, то этот четырехугольник – параллелограмм.
- Если две противоположные стороны четырехугольника равны и параллельны, то этот четырехугольник параллелограмм.
- Если диагонали четырехугольника делятся точкой пересечения пополам, то этот четырехугольник – параллелограмм.
- Если противоположные углы четырехугольника попарно равны, то этот четырехугольник – параллелограмм.
Доказательство
Докажем первый пункт теоремы.
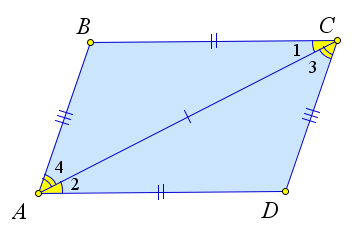
Рассмотрим четырехугольник $ABCD$, в котором $AB=CD, BC=AD$.
Докажем, что $ABCD$ – параллелограмм.
Проведем диагональ $AC$.
Треугольники $\triangle ACB$ и $\triangle ACD$ равны по третьему признаку равенства, следовательно $\angle 3=\angle 4$.
Но так как эти углы являются накрест лежащими при прямых $AB$ и $CD$ и секущей $AC$, то $AB\parallel CD$.
Аналогично $\angle 1=\angle 2$, и следовательно $BC\parallel AD$.
А значит, $ABCD$ – параллелограмм по определению.
Докажем второй пункт теоремы.
Рассмотрим четырехугольник $ABCD$, в котором $AB=CD$ и $AB\parallel
CD$.
Докажем, что тогда $ABCD$ –
параллелограмм.
Проведем диагональ $AC$.
Треугольники $\triangle ACB$ и $\triangle ACD$ равны по второму признаку равенства ($AB=CD$, $AC$ –
общая, $\angle 3=\angle 4$, как накрест лежащие).
Следовательно, $BC=AD$.
Тогда $ABCD$ – параллелограмм по первому пункту теоремы.
Докажем третий пункт теоремы.
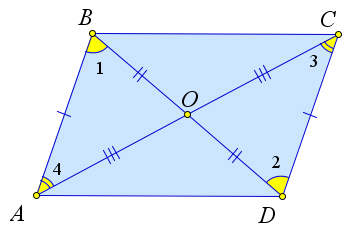
Рассмотрим четырехугольник $ABCD$, в котором диагонали $AC$ и $BD$ пересекаются в точке $O$, и при этом $AO=OC, BO=OD$.
Докажем, что $ABCD$ – параллелограмм.
Действительно, $\angle 1=\angle 2, \angle 3=\angle 4$, как
вертикальные, следовательно, $\triangle AOB=\triangle COD, \triangle BOC=\triangle AOD$ по второму признаку равенства.
Тогда $AB=CD$ и $BC=AD$, и, следовательно, $ABCD$ – параллелограмм по первому пункту теоремы.
Докажем четвертый пункт теоремы.
Обозначим $\angle A=\angle C=\alpha, \angle B=\angle
D=\beta$.
Так как сумма углов четырёхугольника равна $360^\circ$, то
$2\alpha+2\beta=360^\circ$, то есть $\alpha+\beta=180^\circ$.
Но тогда $\angle A+\angle B=180^\circ$, и, так как это односторонние
углы при прямых $AD$ и $BC$ и секущей $AB$, $AD\parallel BC$.
Аналогично, $\angle A+\angle D=180^\circ$, то есть $AB\parallel CD$.
Таким образом $ABCD$ – параллелограмм по определению.