Президентский ФМЛ №239

Векторы называются равными, если их длины равны и они сонаправлены.

1. Каждый вектор равен самому себе.
2. Если вектор $\vec{a}$ равен вектору $\vec{b}$, то вектор $\vec{b}$ равен вектору $\vec{a}$.
3. Два вектора равные третьему вектору, равны.

Первые два свойства очевидно вытекают из определения равенства векторов.

Докажем третье свойство.

Пусть $\vec{a}=\vec{b}$ и $\vec{c}=\vec{b}$.

Тогда $|\vec{a}|=|\vec{b}|$ и $\vec{a}\upuparrows \vec{b}$, а также $|\vec{c}|=|\vec{b}|$ и $\vec{c}\upuparrows \vec{b}$.

Из равенства модулей следует, что $|\vec{a}|=|\vec{c}|$.

А из теоремы \ref{130} вытекает, что $\vec{a}\upuparrows \vec{c}$.

Поэтому $\vec{a}=\vec{c}$.

Если четырехугольник $ABCD$ – параллелограмм, то $\overrightarrow{AB}=\overrightarrow{DC}$.

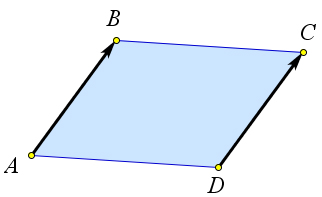
Из того, что $ABCD$ параллелограмм следует, что $AB=CD$ и $AB\parallel CD$.

Кроме того лучи $AB$ и $DC$ лежат по одну сторону от прямой $AD$, следовательно вектора $\overrightarrow{AB}$ и $\overrightarrow{DC}$ сонаправлены и равны по модулю.

Таким образом $\overrightarrow{AB}=\overrightarrow{DC}$.

Если $\overrightarrow{AB}=\overrightarrow{CD}$, то $\overrightarrow{AC}=\overrightarrow{BD}$.

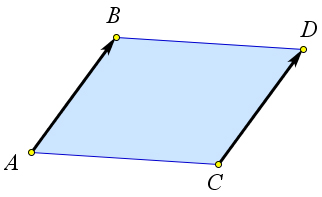
Из равенства векторов $\overrightarrow{AB}$ и $\overrightarrow{CD}$ следует, что $AB=CD$ и либо $AB\parallel CD$, либо точки $A, B, C, D$ лежат на одной прямой.

В первом случае, по признаку, четырехугольник $ABDC$ будет являться параллелограммом.

Следовательно, по теореме $\overrightarrow{AC}=\overrightarrow{BD}$.

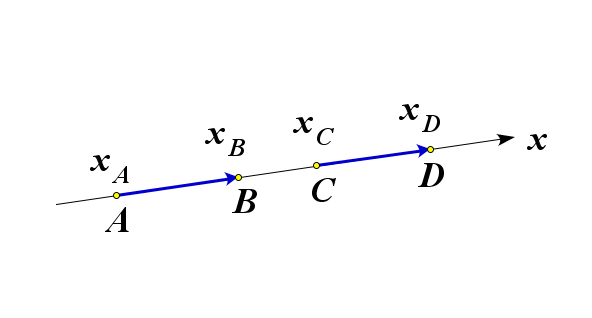
Во втором случае введем на прямой $AB$ координату $x$. Пусть числа $x_A, x_B, x_C, x_D$ – координаты точек $A,B,C,D$ соответственно. Тогда условие $\overrightarrow{AB}=\overrightarrow{CD}$ означает, что выполнено равенство $x_B-x_A=x_D-x_C$.

Здесь равенство модулей чисел $x_B-x_A$ и $x_D-x_C$ означает, что $AB=CD$, а совпадение их знаков – что $\overrightarrow{AB}\upuparrows\overrightarrow{CD}$.

Но тогда $x_C-x_A=x_D-x_B$, что и означает $\overrightarrow{AC}\upuparrows\overrightarrow{BD}$.