Содержание
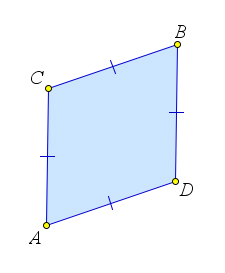
Ромб
Определение
Замечание
Ромб является частным случаем параллелограмма, так как его противоположные стороны попарно равны (третий признак).
Замечание
Ромб наследует все свойства параллелограмма.
Свойства ромба
Доказательство
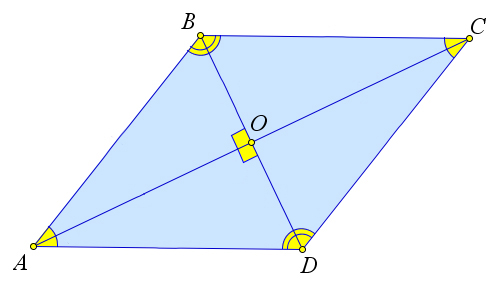
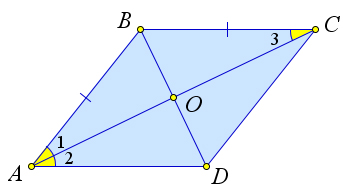
Рассмотрим ромб $ABCD$, в котором диагонали $AC$ и $BD$ пересекаются
в точке $O$.
Докажем, что они перпендикулярны и являются биссектрисами углов ромба.
Действительно, так как $ABCD$ – частный случай параллелограмма, то диагонали точкой пересечения делятся пополам, то есть $AO=OC, BO=OD$.
Тогда, так как $AB=BC=CD=DA$, то $\triangle AOB=\triangle BOC=\triangle COD=\triangle AOD$ по третьему признаку равенства.
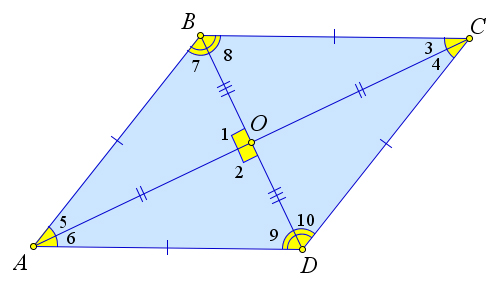
Тогда $\angle 1=\angle 2=90^\circ$, так как это смежные углы.
Кроме того, $\angle 3=\angle 4=\angle 5=\angle 6$, $\angle 7=\angle 8=\angle 9=\angle 10$.
Таким образом диагонали перпендикулярны и являются биссектрисами углов ромба.
Следствие
Диагонали ромба разбивают его на четыре равных прямоугольных треугольника.
Признаки ромба
- Если диагонали параллелограмма взаимно перпендикулярны, то этот параллелограмм – ромб.
- Если одна из диагоналей параллелограмма является биссектрисой его угла, то этот параллелограмм – ромб.
- Если в четырёхугольнике $ABCD$ диагональ $AC$ является биссектрисой углов $\angle A$ и $\angle C$, а диагональ $BD$ является биссектрисой углов $B$ и $D$, то $ABCD$ – ромб.
Доказательство
Докажем первый пункт теоремы.
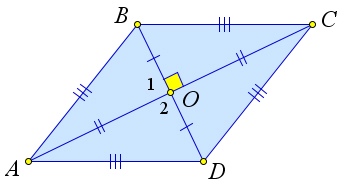
Рассмотрим параллелограмм $ABCD$, в котором $AC\perp BD$.
Докажем, что $ABCD$ – ромб.
В параллелограмме диагонали точкой пересечения делятся пополам, следовательно, $AO=OC, BO=OD$.
Кроме того, $\angle 1=\angle 2=90^\circ$.
Тогда $\triangle AOB=\triangle AOD$ по первому признаку равенства.
Следовательно $AB=AD$.
А так как $ABCD$ – параллелограмм, то $BC=AD=AB=CD$, то есть $ABCD$ – ромб.
Докажем второй пункт теоремы.
Рассмотрим параллелограмм $ABCD$, в котором диагональ $AC$ является биссектрисой угла $\angle A$, то есть $\angle 1=\angle 2$.
Докажем, что $ABCD$ – ромб.
$\angle 2=\angle 3$, как накрест лежащие, следовательно, $\angle 1=\angle 3$.
То есть $\triangle ABC$ – равнобедренный и $AB=BC$.
А так как $ABCD$ – параллелограмм, то $AB=CD, BC=AD$, то есть $AB=BC=CD=AD$, и $ABCD$ – ромб.
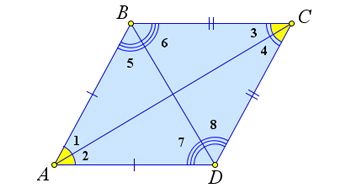
Докажем третий пункт теоремы
Заметим, что $\triangle ABC=\triangle ADC$ по второму признаку ($\angle 1=\angle 2, \angle 3=\angle 4$, $AC$ – общая).
Тогда $\angle B=\angle D$, а следовательно, равны и их половины: $\angle 5=\angle 6=\angle7=\angle 8$.
Но тогда треугольники $\triangle ABD$ и $\triangle BCD$ – равнобедренные: $AB=AD, BC=CD$.
Кроме того $\triangle ABD=\triangle BCD$ по второму признаку ($BD$ – общая, $\angle 5=\angle6, \angle 7=\angle 8$).
А значит $AB=BC$ и $AD=CD$.
Таким образом все стороны четырёхугольника равны между собой: $AB=BC=CD=DA$.