Содержание
Теорема Птолемея
Около четырехугольника можно описать окружность тогда и только тогда, когда произведение его диагоналей равно сумме произведений его противоположных сторон.
Доказательство
Докажем прямую теорему
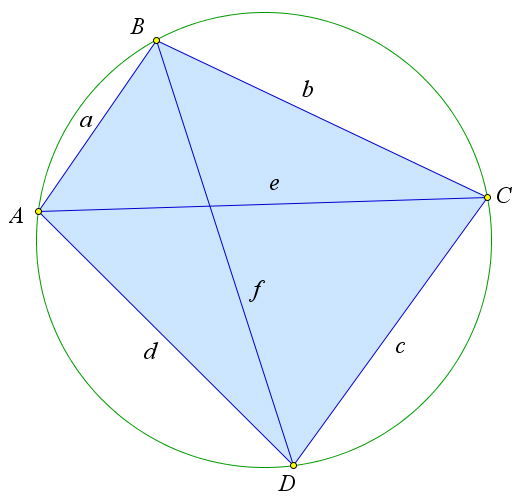
Рассмотрим четырёхугольник $ABCD$ вписанный в окружность.
Тогда $\angle ABC+\angle ADC=180^\circ$, и, следовательно, косинусы этих углов противоположны.
Тогда $\cos{\angle ABC}+\cos{\angle ADC}=0$.
Из треугольников $ABC$ и $ADC$ по теореме косинусов имеем
$\cos{\angle ABC}=\dfrac{a^2+b^2-e^2}{2ab}, \cos{\angle ADC}=\dfrac{d^2+c^2-e^2}{2dc}$.
Сумма этих косинусов равна нулю, то есть $\dfrac{a^2+b^2-e^2}{2ab}+\dfrac{d^2+c^2-e^2}{2dc}=0.$
Домножив последнее равенство на $2abcd$, получим: $a^2dc+b^2dc-e^2dc+d^2ab+c^2ab-e^2ab=0$.
Выразим $e^2$ из последнего равенства: $e^2=\dfrac{ab(d^2+c^2)+dc(a^2+b^2)}{ab+dc}=\dfrac{(ac+bd)(ad+bc)}{ab+cd}$.
Аналогично из треугольников $ABD$ и $BCD$ получаем $f^2=\dfrac{(ab+cd)(ac+bd)}{ad+bc}$.
Отсюда $(ef)^2=(ac+bd)^2$, или $ef=ac+bd$.
Докажем обратную теорему.
Пусть выполнено равенство $AB\cdot CD+BC\cdot AD=AC\cdot BD$.
Докажем, что тогда около четырёхугольника $ABCD$ можно описать окружность.
Обозначим через $R$ радиус окружности, описанной около треугольника $ABC$.
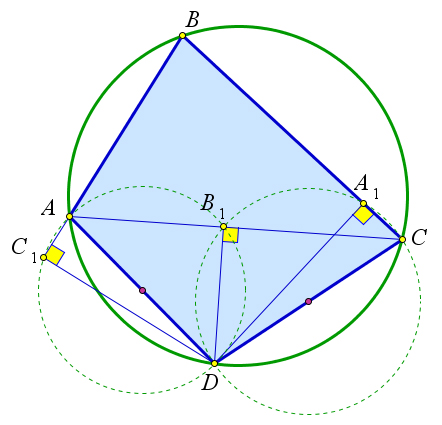
Из точки $D$ опустим перпендикуляры на прямые $AB, BC$ и $AC$ и обозначим точки пересечения этих прямых и перпендикуляров к ним через $C_1, A_1$ и $B_1$ соответственно.
Отрезок $CD$ виден из точек $A_1$ и $B_1$ под углом $90^\circ$, следовательно, точки $A_1$ и $B_1$ лежат на окружности с диаметром $CD$.
По обобщённой теореме синусов для треугольника $A_1CB_1$ получаем: $A_1B_1=CD\sin{\a BCA}$.
По теореме синусов для треугольника $ABC$ имеем $AB=2R\sin{\a BCA}$.
Поделив последние два равенства друг на друга, получим $A_1B_1=\frac{CD\cdot AB}{2R}$.
Таким же образом, рассматривая треугольники $B_1CC_1$ и $A_1CC_1$, получим соотношения $B_1C_1=\dfrac{BC\cdot AD}{2R}, A_1C_1=\dfrac{AC\cdot BD}{2R}$.
Отсюда, подставляя эти выражения в исходное равенство, имеем $2R(A_1B_1+B_1C_1)=C_1A_1\cdot2R$.
Сократив на $2R$, получим $C_1A_1=A_1B_1+B_1C_1$, откуда следует, что точки $A_1, B_1$ и $C_1$ лежат на одной прямой.
Докажем теперь, что из этого следует, что около четырёхугольника $ABCD$ можно описать окружность.
Построим окружности на отрезках $AD$ и $CD$ как на диаметрах.
Первая из них проходит через точки $B_1$ и $C_1$ (углы $AB_1D$ и $AC_1D$ прямые), а вторая – через точки $A_1$ и $B_1$ ($\angle CB_1D=\angle CA_1D=90^\circ$).
По теореме о вписанном угле $\displaystyle\angle ADC_1=\angle AB_1C_1=\dfrac{1}{2}\buildrel\,\,\frown\over{AC_1}$, где дуга берётся на окружности, описанной около $AC_1DB_1$.
Аналогично $\displaystyle\angle A_1DC=\angle AB_1C=\frac{1}{2}\buildrel\,\,\frown\over{A_1C}$, где дуга берётся на окружности, описанной около $A_1CDB_1$.
Но так как углы $AB_1C_1$ и $A_1B_1C$ равны, как вертикальные, то $\angle ADC_1=\angle CDA_1$.
Тогда в прямоугольных треугольниках $DAC_1$ и $DCA_1$ есть равные острые углы $\angle ADC_1=\angle CDA_1$, а значит и другие острые углы равны между собой: $\angle DAC_1=\angle DCA_1$.
Тогда, учитывая, что углы $\angle DAB$ и $\angle DAC_1$ – смежные, получим $\angle DAB+\angle DCB=\angle DAB+\angle DCA_1=180^\circ -\angle DAC_1+\angle DCA_1=180^\circ$.
Следовательно, около четырёхугольника $ABCD$ можно описать окружность.
Другой способ доказательства прямой теоремы
Обозначим диагонали $AC$ и $BD$ вписанного четырехугольника $ABCD$ соответственно $d_1$ и $d_2$, стороны $АВ, ВС, CD, DA$ – $a, b, c, d$, дуги $АВ$ и $CD$ – $\alpha$ и $\gamma$, угол между прямыми $АC$ и $BD$ – $\varphi$. Нужно доказать, что $d_1 d_2=ac+bd$.
Вычислим удвоенную площадь $2S$ четырехугольника $ABCD$ разными способами.
Первый способ: $2S=d_1 d_2 \sin{\varphi} $, при этом $\varphi=\frac{\alpha+\gamma}{2}$
Второй способ: Отрежем треугольник $АВС$ от четырехугольника и приложим его к диагонали $АС$.
Получим четырехугольник $АВ_1СD$, равновеликий четырехугольнику $ABCD$, в котором стороны $a$ и $c$, $b$ и $d$ стали соседними и который вписан в ту же окружность, так как углы $\angle АВС$ и $\angle АВ_1С$ равны между собой.
Теперь вычислим удвоенную площадь этого четырехугольника, разделив его диагональю $В_1D$ на два треугольника.
Получим $2S=bd\sin{A}+ac\sin{C}$.
Угол $\angle А$ вписан в окружность и измеряется половиной дуги $\alpha+\gamma$. Так как углы $\angle А$ и $\angle С$ в сумме составляют развернутый, то их синусы равны.
Поэтому $2S=(ac+bd)\sin{\frac{\alpha+\gamma}{2}}$. Сравнивая полученную формулу с формулой $2S=d_1 d_2 \sin{\varphi}$ Получаем $d_1 d_2=ac+bd$
Следствие
Площадь вписанного четырехугольника, диагонали которого перпендикулярны вычисляется по формуле $S=\dfrac{ac+bd}{2}$.
Доказательство
Площадь четырёхугольника выражается через диагонали по формуле $S=\dfrac{1}{2}d_1d_2\sin{\varphi}$.
Но так как $\varphi=90^\circ$, то есть $\sin{\varphi}=1$, а по теореме Птолемея $d_1d_2=ac+bd$, то $S=\frac{1}{2}d_1d_2\sin{\varphi}=\dfrac{ac+bd}{2}$.