math-public:uravnenie-po-napravlyayushchemu-vektoru-i-tochke
Уравнение по направляющему вектору и точке
$\dfrac{x-x_0}{p}=\dfrac{y-y_0}{q}$, при условии, что $p\neq0, q\neq 0$;
Доказательство
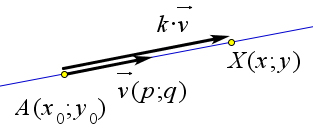
Пусть точка $A$ имеет координаты $(x_0;y_0)$, вектор $\vec{v}$ имеет координаты $(p;q)$.
Пусть произвольная точка $X$ искомой прямой имеет координаты $(x;y)$.
Кроме того, так как вектора $\overrightarrow{AX}$ и $\vec{v}$ коллинеарны, то $\overrightarrow{AX}=k\cdot \vec{v}$, или в координатах $(x-x_0;y-y_0)=(kp;kq)$.
Тогда $x-x_0=kp$ и $y-y_0=kq$.
Выразив из обоих равенств число $k$, получим $k=\frac{x-x_0}{p}=\frac{y-y_0}{q}$, то есть $\frac{x-x_0}{p}=\frac{y-y_0}{q}$.
math-public/uravnenie-po-napravlyayushchemu-vektoru-i-tochke.txt · Последнее изменение: 2016/05/09 14:29 — labreslav