math-public:uravnenie-po-normali-i-tochke
Уравнение по нормали и точке
$a(x-x_0)+b(y-y_0)=0$.
Доказательство
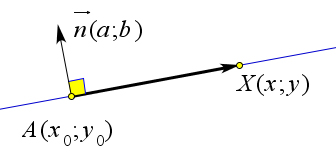
Пусть вектор $n$ с координатами $(a;b)$ является нормалью к прямой $l$, проходящей через точку $A(x_0;y_0)$.
Тогда для любой точки $X$ данной прямой $\overrightarrow{AX}$ будет перпендикулярен $\vec{n}$, следовательно $\overrightarrow{AX}\cdot \vec{n}=0$.
Расписав это равенство в координатах, получим $a(x-x_0)+b(y-y_0)=0$.
math-public/uravnenie-po-normali-i-tochke.txt · Последнее изменение: 2016/05/09 14:01 — labreslav