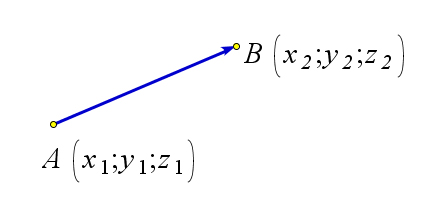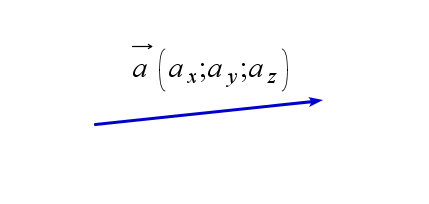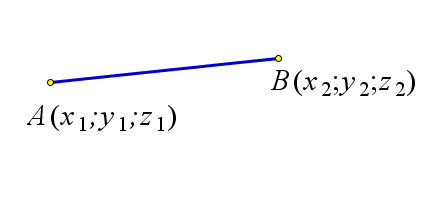Президентский ФМЛ №239

Это старая версия документа!

−Содержание

Определители
Основные формулы
Углы
Расстояния
Объёмы

Определители

Два на два

$\left|\begin{array}{cc} a&b\\c&d\end{array}\right|=a\cdot d-b\cdot c$

Три на три

$\left|\begin{array}{ccс} x_1&x_2&x_3\\y_1&y_2&y_3\\z_1&z_2&z_3\end{array}\right|=x_1\cdot\left|\begin{array}{cc}y_2&y_3\\z_2&z_3\end{array}\right|-x_2\cdot\left|\begin{array}{cc} y_1&y_3\\z_1&z_3\end{array}\right|+x_3\cdot\left|\begin{array}{cc} y_1&y_2\\z_1&z_2\end{array}\right|$

Три на три с векторами

$\left|\begin{array}{ccс}\vec{i}&\vec{j}&\vec{k}\\y_1&y_2&y_3\\z_1&z_2&z_3\end{array}\right|=\vec{i}\cdot\left|\begin{array}{cc}y_2&y_3\\z_2&z_3\end{array}\right|-\vec{j}\cdot\left|\begin{array}{cc} y_1&y_3\\z_1&z_3\end{array}\right|+\vec{k}\cdot\left|\begin{array}{cc}y_1&y_2\\z_1&z_2\end{array}\right|=\left(y_2z_3-y_3z_2;-y_1z_3+y_3z_1; y_1z_2-y_2z_1\right)$

Основные формулы

Координаты вектора	Длина вектора	Середина отрезка	Точка на отрезке
$1$	$1$	$1$	$1$
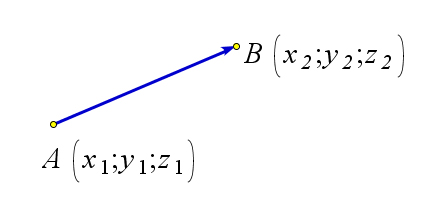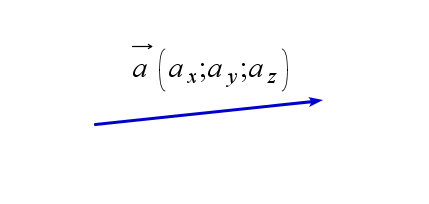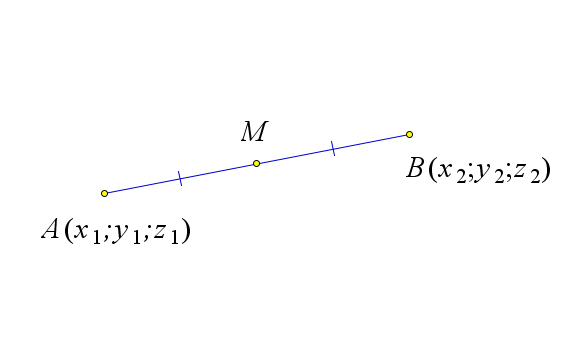
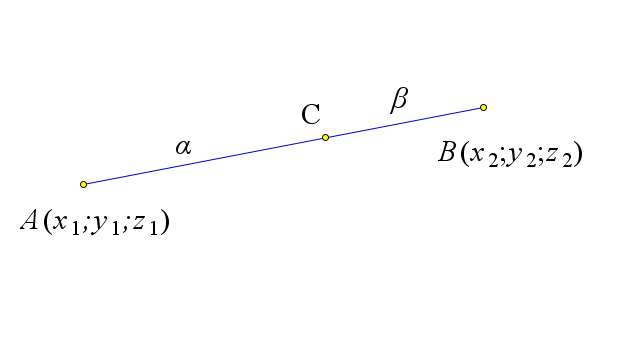
$\overrightarrow{AB}=(x_1-x_2; y_1-y_2;z_1-z_2)$ $A(x_1;y_1;z_1);$ $B(x_2;y_2;z_2)$	$\|\vec{a}\|=\sqrt{a_x^2+a_y^2+a_z^2}$ $\vec{a}=(a_x;a_y;a_z)$	$M=\left(\dfrac{x_1+x_2}{2}, \dfrac{y_1+y_2}{2}, \dfrac{z_1+z_2}{2}\right)$	$C=\left(\dfrac{\beta x_1+\alpha x_2}{\alpha+\beta}, \dfrac{\beta y_1+\alpha y_2}{\alpha+\beta}, \dfrac{\beta z_1+\alpha z_2}{\alpha+\beta}\right)$

Скалярное произведение	Проекция вектора на вектор	Угол между векторами
$1$	$1$	$1$
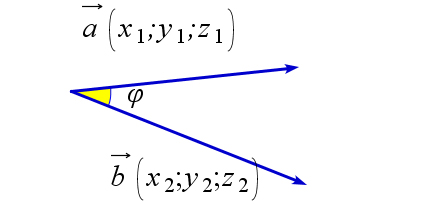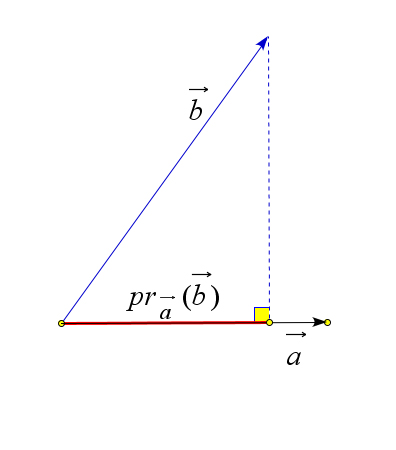
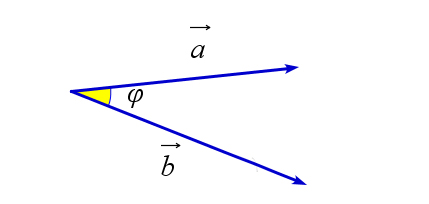
$\vec{a}\cdot\vec{b}=x_1x_2+y_1y_2+z_1z_2$ $\vec{a}=(x_1;y_1;z_1);$ $\vec{b}=(x_2;y_2;z_2)$	$pr_{\vec{a}}(\vec{b})=\left\|\dfrac{\vec{a}\cdot\vec{b}}{\|\vec{a}\|}\right\|$	$\angle(\vec{a},\vec{b})=\arccos\left(\dfrac{\vec{a}\cdot\vec{b}}{\|\vec{a}\|\cdot\|\vec{b}\|}\right)$

Нормаль к плоскости	Смешанное произведение векторов	Векторное произведение
$1$	$1$	$1$
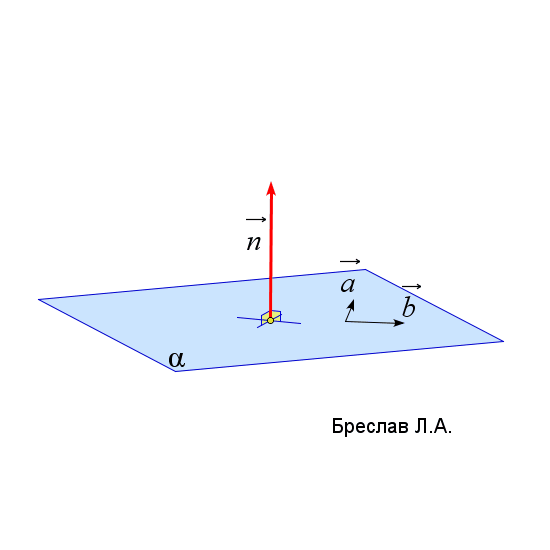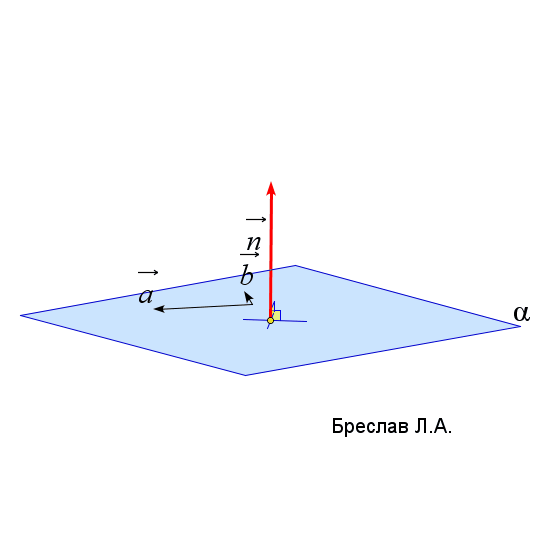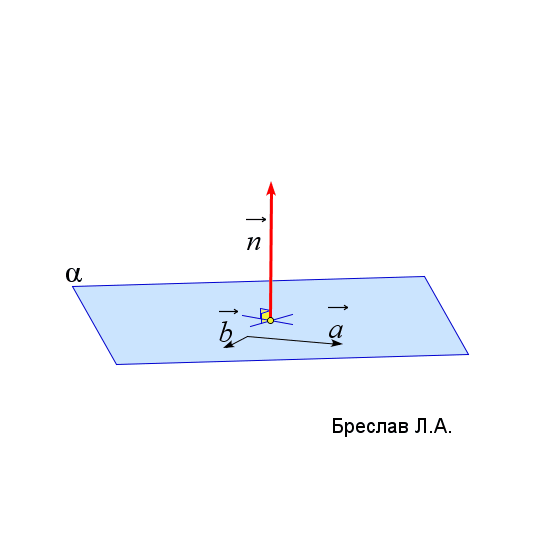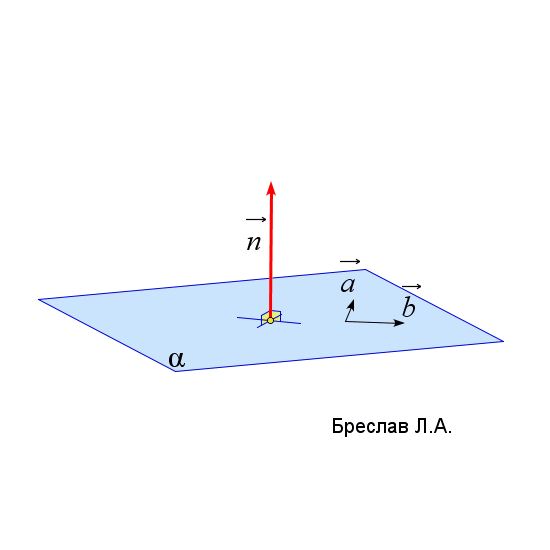$\vec{n}_\alpha=\left\|\begin{array}{ccc} \vec{i}&\vec{j}&\vec{k}\\ a_x&a_y&a_z\\ b_x&b_y&b_z\end{array}\right\|$ $\vec{a}$ и $\vec{b}$ лежат в плоскости $\alpha$ $\vec{a}=(a_x;a_y;a_z), \vec{b}=(b_x;b_y;b_z)$	$(\vec{a},\vec{b},\vec{c})=\left\|\begin{array}{ccc} a_x&a_y&a_z\\ b_x&b_y&b_z\\ c_x&c_y&c_z\end{array}\right\|$ $\vec{a}=(a_x;a_y;a_z), \vec{b}=(b_x;b_y;b_z), \vec{c}=(c_x;c_y;c_z)$	$\vec{a}\times\vec{b}=\left\|\begin{array}{ccc} \vec{i}&\vec{j}&\vec{k}\\ a_x&a_y&a_z\\ b_x&b_y&b_z\end{array}\right\|$ $\vec{a}=(a_x;a_y;a_z), \vec{b}=(b_x;b_y;b_z)$

Углы

Угол между двумя прямыми	Угол между прямой и плоскостью	Угол между двумя плоскостями
$1$	$1$	$1$
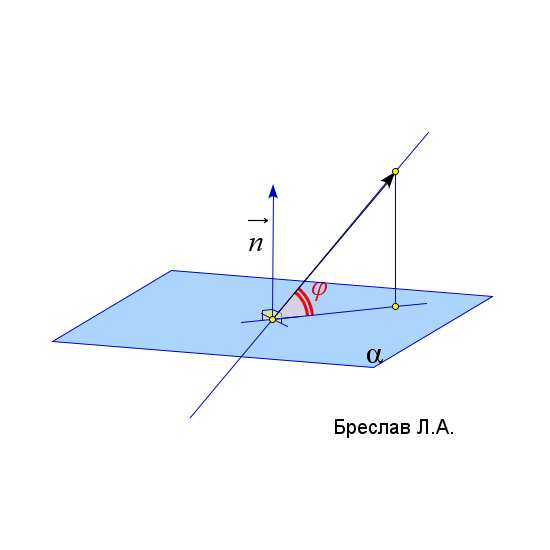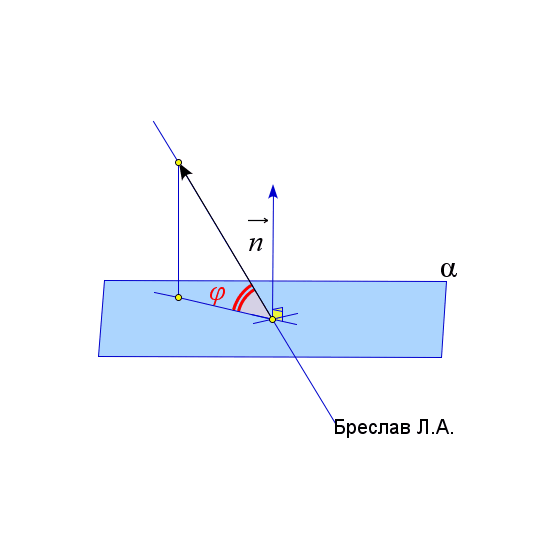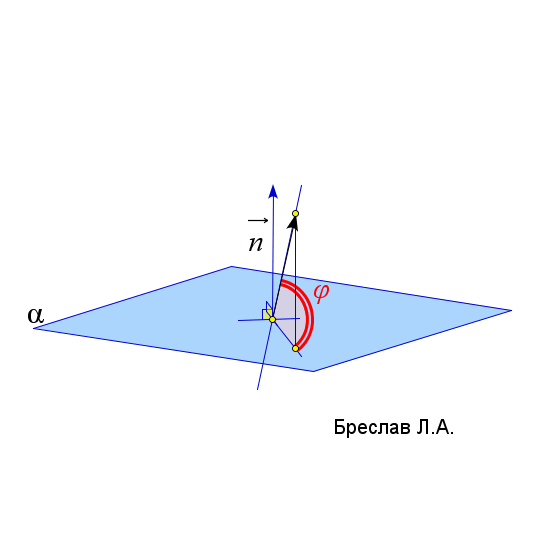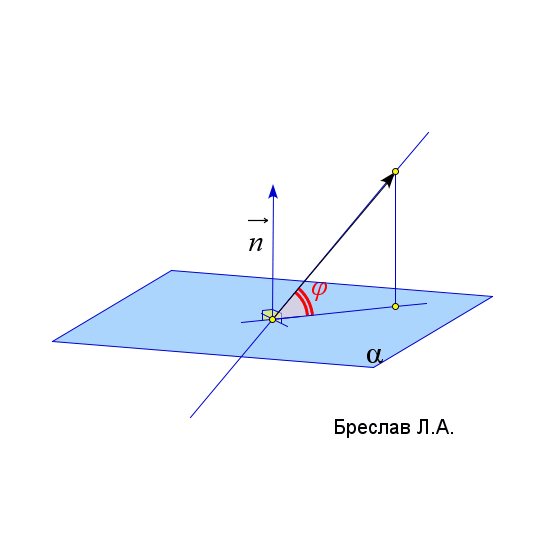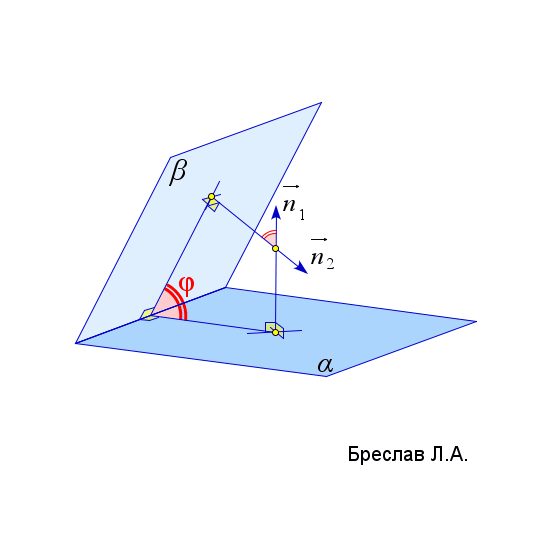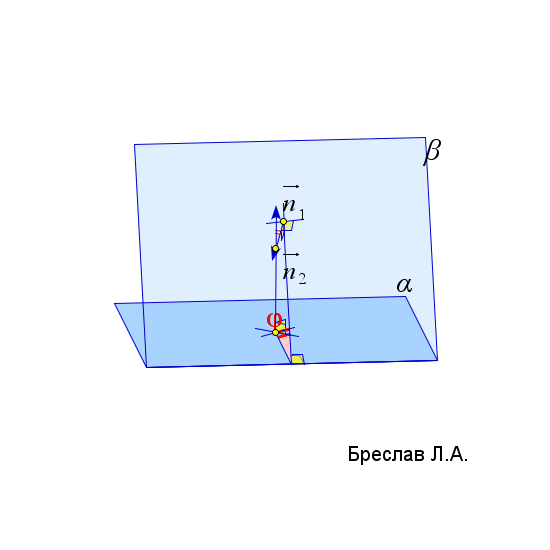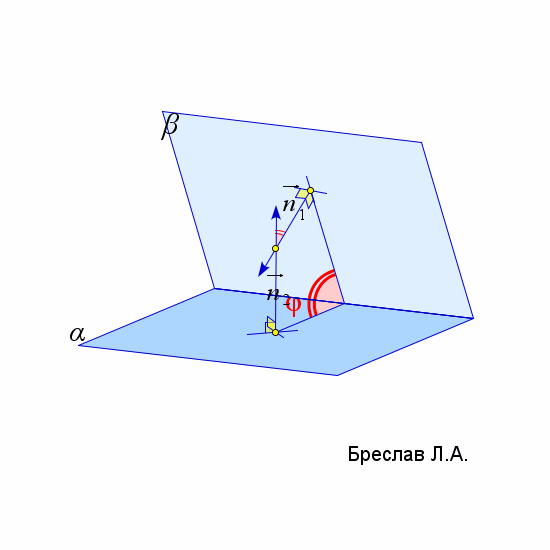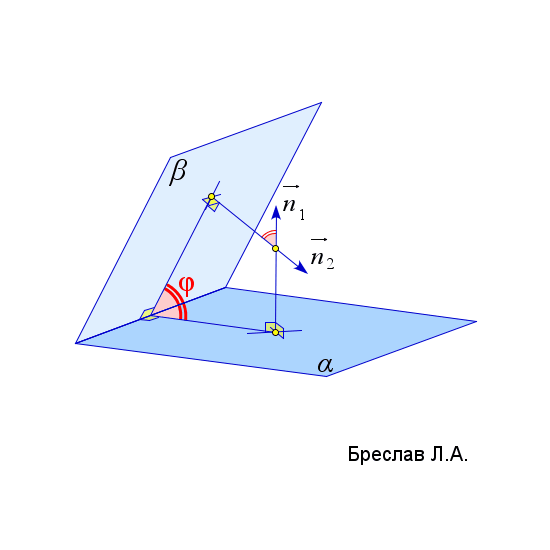
$\angle (l_1;l_2)=arccos\left(\left\|\dfrac{\vec{a}\cdot\vec{b}}{\|\vec{a}\|\cdot\|\vec{b}\|}\right\|\right)$ $\vec{a}$ и $\vec{b}$ – направляющие вектора прямых $l_1$ и $l_2$	$\angle(l;\alpha)=arcsin\left(\left\|\dfrac{\vec{a}\cdot\vec{n}_\alpha}{\|\vec{a}\|\cdot\|\vec{n}_\alpha\|}\right\|\right)$ $\vec{a}$ и $\vec{b}$ лежат в плоскости $\alpha$ $\vec{c}$ соединяет точку $A$ и любую точку из плоскости $\alpha$	$\angle(\alpha;\beta)=arccos\left(\left\|\dfrac{\vec{n}_1\cdot\vec{n}_2}{\|\vec{n}_1\|\cdot\|\vec{n}_2\|}\right\|\right)$ $\vec{n}_1$ и $\vec{n}_2$ – нормали к плоскостям $\alpha$ и $\beta$

Расстояния

Расстояние между двумя точками	Расстояние от точки до прямой	Расстояние от точки до плоскости	Расстояние между двумя скрещивающимися прямыми
$1$	$1$	$1$	$1$
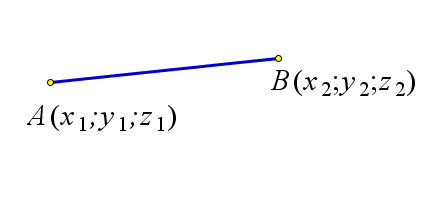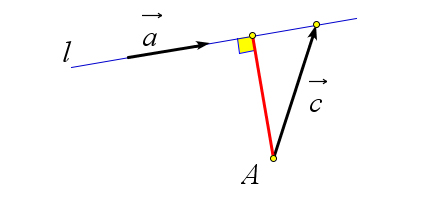
$\|AB\|=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}$ $A(x_1;y_1;z_1)$ $B(x_2;y_2;z_2)$	$\rho(A;l)=\dfrac{\|\vec{a}\times\vec{c}\|}{\|\vec{a}\|}$	$\rho(A;\alpha)=\left\|\dfrac{(\vec{a},\vec{b},\vec{c})}{\|\vec{a}\times\vec{b}\|}\right\|$ $\vec{a}$ и $\vec{b}$ лежат в плоскости $\alpha$ $\vec{c}$ соединяет точку $A$ и любую точку из плоскости $\alpha$	$\rho(l_1;l_2)=\left\|\dfrac{(\vec{a},\vec{b},\vec{c})}{\|\vec{a}\times\vec{b}\|}\right\|$ $\vec{a}$ и $\vec{b}$ – направляющие вектора прямых $\vec{c}$ произвольный вектор, соединяющий прямые $l_1$ и $l_2$

Объёмы

Объём тетраэдра	Объём параллелепипеда
$1$	$1$
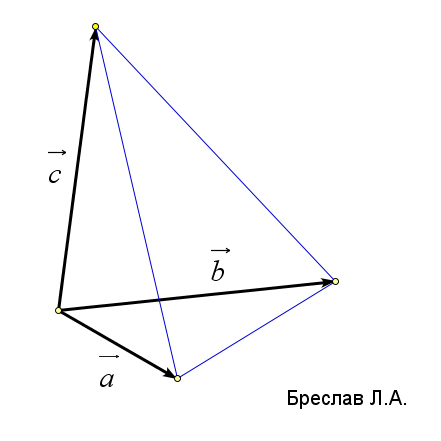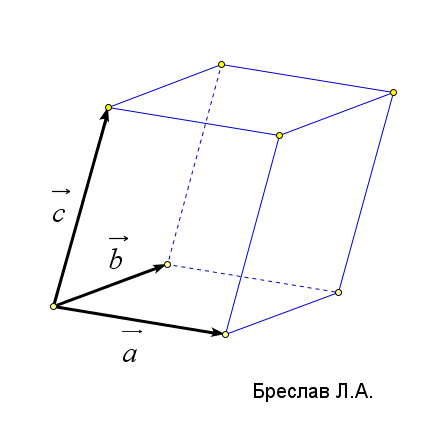$V=\dfrac{1}{6}\left\|(\vec{a}, \vec{b}, \vec{c})\right\|$	$V=\left\|(\vec{a}, \vec{b}, \vec{c})\right\|$