Президентский ФМЛ №239

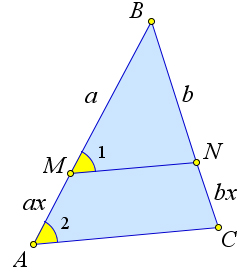
Пусть на сторонах $AB$ и $BC$ треугольника $ABC$ отмечены точки $M$ и $N$ соответственно. Тогда

1. Если $BM:MA=BN:NC$, то $MN\parallel AC$;
2. Если $MN\parallel AC$, то $BM:MA=BN:NC$;

Пусть $BM=a, MA=xa, BN=b, NC=xb$.

Тогда $\dfrac{BM}{BA}=\dfrac{a}{a+ax}=\dfrac{1}{1+x}=\dfrac{b}{b+bx}=\dfrac{BN}{BC}$.

Тогда треугольники $BMN$ и $ABC$ подобны по второму признаку подобия треугольников, так как $\angle B$ – общий.

Следовательно, $\angle 1=\angle 2$, а так как это соответственные углы при секущей $AB$, то $MN\parallel AC$.

Так как $MN\parallel AC$, то $\angle 1=\angle 2$, а поскольку $\angle B$ – общий, то треугольники $BMN$ и $ABC$ подобны.

Тогда $\dfrac{BM}{BA}=\dfrac{BN}{BC}$, откуда $\dfrac{BM}{BM+MA}=\dfrac{1}{1+\dfrac{MA}{BM}}=\dfrac{1}{1+\dfrac{NC}{BN}}$.

Следовательно, $\dfrac{MA}{BM}=\dfrac{NC}{BN}$.

Параллельные прямые отсекают на секущих пропорциональные отрезки.

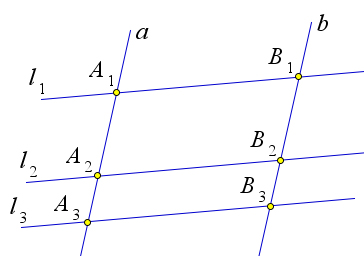
Пусть параллельные прямые $l_1, l_2, l_3$ пересекают прямые $a$ и $b$ в точках $A_1, A_2, A_3$ и $B_1, B_2, B_3$ соответственно.

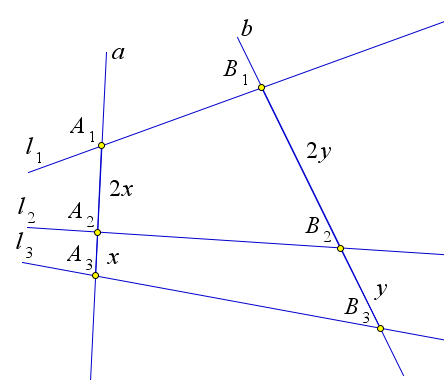
Пусть при этом $A_1A_2:A_2A_3=x$.

Докажем, что тогда $B1B_2:B_2B_3=x$.

Рассмотрим случай, когда прямые $a$ и $b$ параллельны.

Тогда $A_2A_1B_1B_2$ и $A_3A_2B_2B_3$ – параллелограммы, следовательно, $A_1A_2=B_1B_2$ и $A_2A_3=B_2B_3$, и так как $A_1A_2:A_2A_3=B_1B_2:B_2B_3=x$.

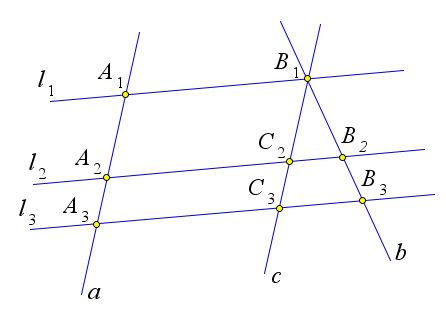
Рассмотрим случай, когда прямые $a$ и $b$ не параллельны.

Проведем через точку $B_1$ прямую $c$, параллельную прямой $a$.

Пусть прямые $l_2,l_3,l_4$ и прямая $c$ пересекаются в точках $C_2, C_3, C_4$.

По первому случаю $B_1C_2:C_2C_3=x$, кроме того $B_2C_2\parallel B_3C_3$.

Тогда по второму пункту леммы $B_1C_2:C_2C_3=B_1B_2:B_2B_3=x$.

Следующее утверждение неверно:
пусть прямые $l_1, l_2, l_3$ пересекают прямые $a$ и $b$ в точках $A_1,A_2,A_3$ и $B_1,B_2,B_3$ соответственно. Тогда из того, что $A_1A_2:A_2A_3=B_1B_2:B_2B_3$ следует, что $l_1\parallel l_2\parallel l_3$.