Президентский ФМЛ №239

1. Синус острого угла равен отношению перпендикуляра к наклонной.
2. Синус тупого угла равен синусу смежного острого угла.
3. Синус прямого угла равен единице.
4. Синус развернутого угла равен нулю.

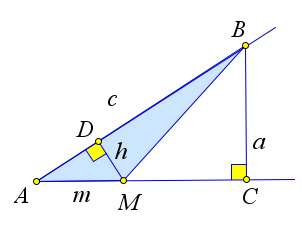
Пусть из точки $B$, лежащей на стороне $p$ острого угла $A$, опущен перпендикуляр $BC$ на сторону $q$ этого угла. Тогда отношение перпендикуляра $BC$ к наклонной $BA$ не зависит от выбора точки $B$.

На стороне $q$ выберем любую точку $M$.

Выразим площадь $S$ треугольника $ABM$ двумя способами.

С одной стороны, $S=\dfrac{1}{2}ma$, где $a=BC, m=AM$.

C другой стороны, $S=\dfrac{1}{2}ch$, где $h=MD$ – высота треугольника $ABM$ и $c=BA$.

Поэтому $ma=ch$ или $\dfrac{a}{c}=\dfrac{h}{m}$.

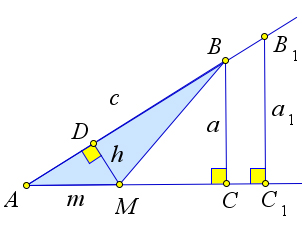
Если на стороне $p$ взять другую точку $B_1$ и повторить проведенные рассуждения, то снова получим, что $\dfrac{a_1}{c_1}=\dfrac{h}{m}$, где $a_1=B_1C, c_1=AB_1$.

Поэтому $\dfrac{a_1}{c_1}=\dfrac{a}{c}$.

Отношение перпендикуляра к наклонной не зависит от того, на какую сторону угла опущен перпендикуляр.

Действительно, пусть, как и раньше, $M$ – точка на стороне $q$ угла $A$ и $MD\perp p$.

Вернемся к равенству $\dfrac{a}{c}=\dfrac{h}{m}$

В правой части этого равенства стоит отношение перпендикуляра к наклонной, которое с выбором точки $M$ не связано.

Значит правая часть этого равенства от выбора точки $M$ не зависит.

Если на стороне $p$ взять точки $B$ и $B_1$ и опустить из них перпендикуляры $BC$ и $B_1C_1$ к стороне $q$ угла $A$, то треугольники $ABC$ и $AB_1C_1$ будут подобны по двум углам.

Следовательно, $\dfrac{BC}{AB}=\dfrac{B_1C_1}{AB_1}$.

Отношение перпендикуляра к наклонной не зависит от того, на какую сторону угла опущен перпендикуляр.

Действительно, пусть, как и раньше, $M$ – точка на стороне $q$ угла $A$ и $MD\perp p$.

Треугольники $ADM$ и $ABC$ подобны по двум углам ($\angle A$ – общий).

Следовательно, $\dfrac{MD}{AM}=\dfrac{BC}{AB}$, а отношение, стоящее в правой части этого равенства не зависит от выбора точки $M$.

Синусы углов, имеющих равные величины, равны.

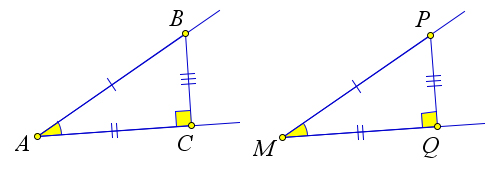
Возьмем два равных острых угла: $\angle A$ и $\angle M$.

Из некоторой точки $B$ на стороне угла $A$ опустим перпендикуляр $BC$ на другую сторону угла $A$.

Получим прямоугольный треугольник $ABC$.

Отложим на сторонах угла $M$ отрезки $MP=AB$ и $MQ=AC$.

Тогда $\triangle MPQ=\triangle ABC$ по первому признаку равенства.

Поэтому $\angle Q=\angle C=90^\circ$.

Итак $PQ$ – перпендикуляр, опущенный из точки $P$ одной стороны угла $M$ на другую его сторону.

Но тогда $\sin{\angle A}=\dfrac{BC}{AB}=\dfrac{PQ}{PM}=\sin{\angle M}$.