Две прямые на плоскости называются параллельными, если они не имеют общих точек.

Через данную точку можно провести не более одной прямой, параллельной данной.

Если прямая пересекает одну из двух данных параллельных прямых, то она пересекает и вторую.

Пусть прямые $a$ и $b$ параллельны, и прямая $с$ пересекает прямую $a$ в точке $M$.

Если предположить, что прямая $c$ не пересекает прямую $b$, то получится, что через точку $M$ проходит две прямые, параллельные прямой $a$, что противоречит аксиоме.

Если две прямые параллельны третьей прямой, то они параллельны.

Пусть прямые $a$ и $b$ параллельны прямой $c$. Если предположить, что прямые $a$ и $b$ пересекаются в точке $M$, то получится, что через точку $M$ проходит две прямые, параллельные прямой $c$, что противоречит аксиоме $\ref{aks5}$.

Если две прямые перпендикулярны данной прямой, то они параллельны.

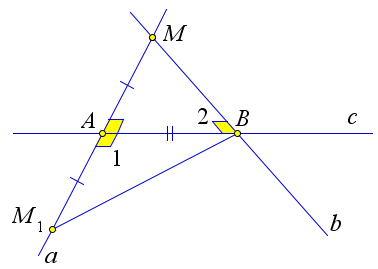
Пусть $a\perp AB, b\perp AB$.

Докажем, что $a\parallel b$.

Предположим противное: $a\cap b = M$.

Выберем на прямой $a$ точку $M_1$ так, чтобы $AM=AM_1$.

Тогда $\triangle ABM=\triangle ABM_1$ по первому признаку равенства треугольников ($AM=AM_1$, $AB$ – общая, $\angle 1=\angle MAB=90^\circ$).

Но тогда $\angle 2=\angle ABM_1=90^\circ$, следовательно, $(\angle 2+\angle ABM_1)=180^\circ$, то есть точки $M,B,M_1$ лежат на одной прямой, а это противоречит аксиоме, так как прямые $BM$ и $a$ пересекаются в двух различных точках $M$ и $M_1$.

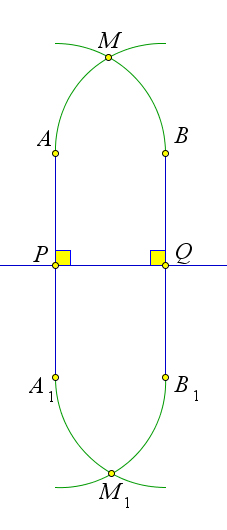
Рассмотрим прямые $AA_1$ и $BB_1$ перпендикулярные прямой $PQ$.

Мысленно перегнем рисунок по прямой $PQ$.

Так как $AA_1\perp PQ$, то луч $PA$ наложится на луч $PA_1$.

Аналогично, луч $QB$ наложится на луч $QB_1$.

Поэтому, если предположить, что прямые $AA_1$ и $BB_1$ пересекаются в точке $M$, то эта точка наложится на некоторую точку $M_1$, также лежащую на этих прямых, что противоречит аксиоме.

1. Если при пересечении двух прямых третьей образуются равные внутренние накрест лежащие углы, то прямые параллельны.
2. Если при пересечении двух прямых третьей образуются равные соответственные углы, то прямые параллельны.
3. Если при пересечении двух прямых третьей сумма односторонних углов равна $180^\circ$, то прямые параллельны.

Пусть при пересечении прямых $a$ и $b$ секущей $AB$ накрест лежащие углы равны: $\angle 1=\angle 2$.

Докажем, что тогда $a\parallel b$.

Если $\angle 1=\angle 2=90^\circ$.

Тогда $a\parallel b$ в силу леммы.

Рассмотрим случай, когда $\angle 1=\angle 2\neq90^\circ$.

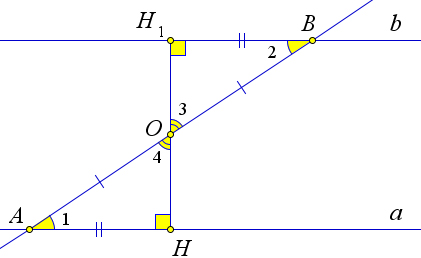
Проведем из точки $O$ – середины отрезка $AB$ – перпендикуляр $OH$ к прямой $a$.

От точки $B$ на прямой $b$ отложим отрезок $BH_1$ равный отрезку $AH$.

Тогда $\triangle AOH=\triangle BOH_1$ по первому признаку равенства треугольников ($AO=OB, AH=BH_1, \angle 1=\angle 2$).

Следовательно, $\angle 3=\angle 4, \angle H=\angle H_1=90^\circ$.

Из равенства $\angle 3=\angle 4$ следует, что точки $H, O$ и $H_1$ лежат на одной прямой.

Из равенства $\angle H=\angle H_1=90^\circ$ следует, что прямые $a$ и $b$ перпендикулярны к прямой $HH_1$, и следовательно, параллельны по лемме.

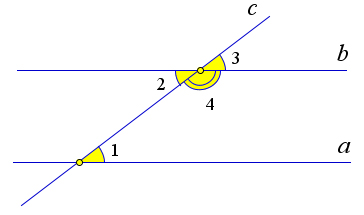
Пусть при пересечении прямых $a$ и $b$ секущей $c$ соответственные углы равны: $\angle 1=\angle 3$.

Покажем, что $a\parallel b$.

Действительно, $\angle 3=\angle 2$, как вертикальные.

Следовательно, $\angle 2=\angle 1$, и прямые $a$ и $b$ параллельны по первому пункту теоремы.

Пусть при пересечении прямых $a$ и $b$ секущей $c$ $\angle 1+\angle 4=180^\circ$.

Покажем, что $a\parallel b$.

Действительно, $\angle 2=180^\circ-\angle 4=\angle 1$.

Следовательно, $\angle 2=\angle 1$, и прямые $a$ и $b$ параллельны по первому пункту теоремы.

Если две параллельные прямые пересечены третьей прямой, то образованные при этом накрест лежащие углы равны, соответственные углы равны, и сумма односторонних углов равна $180^\circ$.

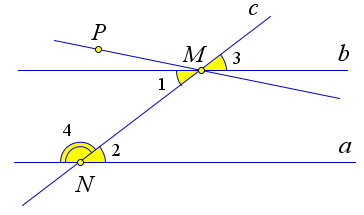
Пусть параллельные прямые $a$ и $b$ пересечены секущей $MN$.

Покажем, что накрест лежащие углы, например $\angle 1$ и $\angle 2$, равны.

Предположим противное, то есть $\angle 1\neq\angle 2$.

Отложим от луча $MN$ угол $\angle PMN$, равный углу $\angle 2$, так, чтобы $\angle PMN$ и $\angle 2$ были накрест лежащими при пересечении $MP$ и $b$ секущей $MN$.

Тогда по теореме $MP\parallel b$.

Тогда через точку $M$ проходит две прямые ($a$ и $MP$) параллельные прямой $b$, а это противоречит аксиоме.

Значит $\angle 1=\angle 2$.

Так как $\angle 3=\angle 1$ как вертикальные, то $\angle 3=\angle 2$, то есть соответственные углы равны.

Так как $\angle 2$ и $\angle 4$ смежные, то $180^\circ=\angle 2+\angle 4=\angle 1+\angle 4$.

То есть сумма односторонних углов равна $180^\circ$.