1. Прямоугольник - это параллелограмм с прямым углом.
2. Прямоугольник - это четырехугольник, у которого все углы прямые.

Пункты 1 и 2 определения прямоугольника эквивалентны.

Действительно, если в параллелограмме есть один прямой угол, то все остальные его углы тоже прямые (так как противоположные стороны параллельны).

Обратно, если в четырехугольнике все углы прямые, то его противоположные стороны параллельны, и, следовательно, это параллелограмм.

Прямоугольник наследует все свойства параллелограмма.

Диагонали прямоугольника равны.

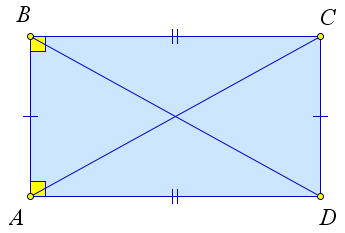
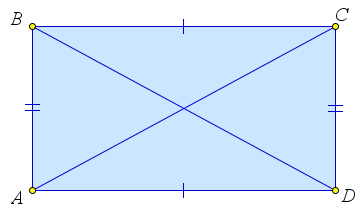
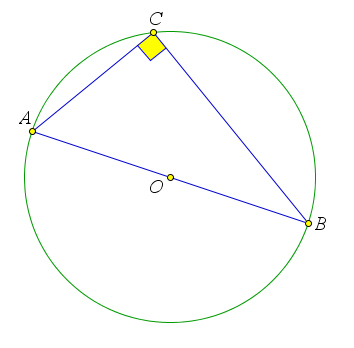
Рассмотрим прямоугольник $ABCD$. Докажем, что $AC=BD$.

Поскольку прямоугольник – это частный случай параллелограмма ,то $BC=AD$.

Тогда треугольники $\triangle ABC$ и $\triangle DAB$ равны по первому признаку ($BC=AD$, $AB$ – общая, $\angle A = \angle B=90^\circ$).

Следовательно, $AC=BD$.

Диагонали прямоугольника разбивают его на четыре равнобедренных треугольника.

Полезно понимать следующую картинку про прямоугольник. (все равные углы, все равные отрезки).

Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.

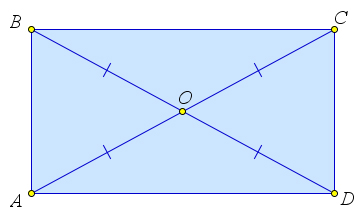
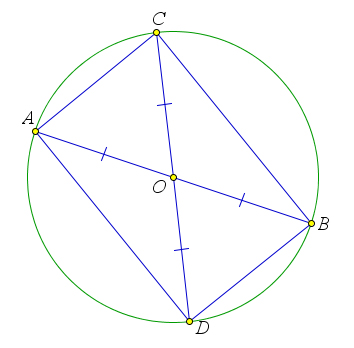
Рассмотрим параллелограмм $ABCD$, в котором $AC=BD$.

Докажем, что этот параллелограмм – прямоугольник.

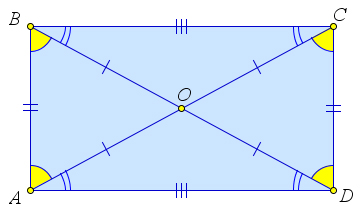
Действительно, треугольники $\tri ABC$ и $\triangle DAB$ равны по третьему признаку ($BC=AD$, $AC=BD$, $AB$ – общая).

Тогда $\angle A=\angle B$. Но поскольку $\angle A+\angle B=180^\circ$, то $\angle A=\angle B=90^\circ$.

Вписанный угол, опирающийся на диаметр, равен $90^\circ$.

Пусть прямая $CO$ пересекает окружность в точке $D$.

Тогда $OA=OB=OC=OD$, так как это радиусы окружности.

Значит диагонали четырехугольника $ABCD$ точкой пересечения делятся пополам, а значит это параллелограмм.

Кроме того диагонали равны, а значит это прямоугольник, то есть $\angle C=90^\circ$.