Содержание
Свойство
Гипотенуза прямоугольного треугольника вдвое больше медианы, проведенной из вершины прямого угла.
Доказательство
Рассмотрим прямоугольный треугольник $ABC$, с прямым углом $C$ и медианой $CM$ (тогда $AM=MB$).
Докажем, что $2\cdot CM=AB$.
Первый способ.
Предположим, что это не так.
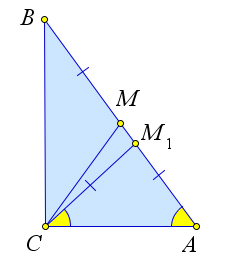
Тогда $CM\neq MA$, и, следовательно, $\angle MCA \neq \angle A$.
Тогда выберем на гипотенузе $AB$ такую точку $M_1$, что $\angle M_1CA = \angle A$ (это возможно по аксиоме).
Тогда $\triangle M_1CA$ – равнобедренный.
Кроме того $\angle B=90^\circ - \angle A=90^\circ - \angle M_1CA=\angle M_1CB$, то есть треугольник $M_1C B$ – равнобедренный, и $M_1C=M_1B$.
Но тогда $M_1B=M_1A$, то есть $M_1$ – середина гипотенузы $AB$, что невозможно.
Второй способ.
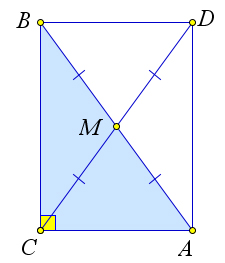
Достроим треугольник $ABC$ до прямоугольника $ABCD$.
Диагонали $AB$ и $CD$ равны и точкой пересечения $M$ делятся пополам.
Следовательно, $2CM=CD=AB$.
Признак
Если медиана треугольника равна половине стороны, к которой она проведена, то треугольник прямоугольный.
Доказательство
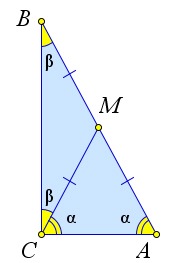
Рассмотрим треугольник $ABC$, в котором $MC$ – медиана, и $MC=MA=MB$.
Докажем, что тогда $ABC$ – прямоугольный.
Действительно, $\triangle MCA$ и $\triangle BMC$ – равнобедренные, следовательно, $\angle A=\angle MCA=\alpha$ и $\angle B=\angle BCM=\beta$.
Тогда $2\alpha+2\beta=180^\circ$.
Откуда получаем, что $\angle C=\alpha+\beta=90^\circ$.