1. Углы при основании равнобедренного треугольника равны.
2. Медиана, высота и биссектриса равнобедренного треугольника, проведенные к основанию, совпадают.

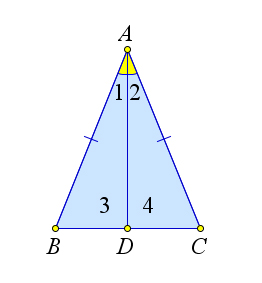
Рассмотрим равнобедренный треугольник $ABC$ с основанием $BC$.

Пусть $AD$ – биссектриса этого треугольника.

Треугольники $ABD$ и $ACD$ равны по первому признаку равенства треугольников $(AB=AC, AD$ – общая, $\angle 1=\angle 2)$.

Следовательно, $\angle B=\angle C$.

Кроме того, $\angle 3=\angle 4$, а поскольку они смежные, то каждый из них является прямым, то есть $AD$ – высота.

Из равенства этих треугольников следует, что $BD=DC$.

Следовательно $AD$ – не только биссектриса и высота, но и медиана.

1. Если два угла треугольника равны, то треугольник равнобедренный.
2. Если медиана треугольника является его высотой, то треугольник равнобедренный.
3. Если биссектриса треугольника является его высотой, то треугольник равнобедренный.
4. Если медиана треугольника является его биссектрисой, то треугольник равнобедренный.

Рассмотрим треугольник $ABC$.

Докажем, что если $\angle B=\angle C$, то $AB=AC$.

Поскольку $\angle B$ и $\angle C$ острые (иначе сумма углов треугольника $ABC$ была бы больше $180^\circ$), то высота, проведенная из вершины $A$ падает на сторону $BC$.

Так как сумма углов треугольника равна $180^\circ$, то $\angle 1=180^\circ-90^\circ-\angle B=180^\circ-90^\circ-\angle C=\angle 2$.

Следовательно, треугольники $ABD$ и $ACD$ равны по второму признаку равенства треугольников $(\angle 1=\angle 2, \angle 3=\angle 4, AD$– общая сторона$)$.

Тогда $AB=AC$, то есть треугольник равнобедренный.

Если предположить, что одна из указанных сторон больше другой, то угол, лежащий против нее, будет больше угла, лежащего против другой стороны, а это противоречит условию (тому, что данные углы равны).

Итак $AB=AC$.

Докажем теперь, что если $AD$ – медиана и высота, то треугольник равнобедренный.

Действительно, так как $BD=DC, \angle 3=\angle 4=90^\circ$, a $AD$ – общая сторона, то треугольники $ABD$ и $ACD$ равны по первому признаку равенства треугольников.

Следовательно, $AB=AC$, то есть треугольник равнобедренный.

Докажем, что если $AD$ – биссектриса и высота для $\triangle ABС$, то треугольник равнобедренный.

Действительно, так как $\angle 1 =\angle 2, \angle 3=\angle 4=90^\circ$, a $AD$ – общая сторона, то треугольники $ABD$ и $ACD$ равны по второму признаку равенства треугольников.

Следовательно, $AB=AC$, то есть треугольник равнобедренный.

Докажем, что если $AD$ – медиана и биссектриса, то треугольник равнобедренный.

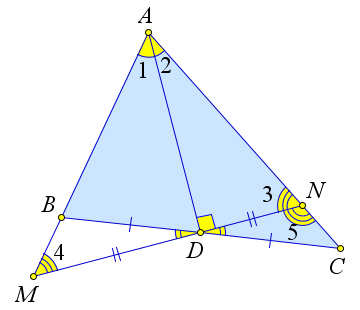
Предположим противное – треугольник $ABC$ не равнобедренный, и, следовательно, $AD$ не высота.

Проведем через точку $D$ прямую $l$ перпендикулярно $AD$.

Обозначим точки пересечения прямой $l$ с прямыми $AB$ и $AC$ как $M$ и $N$ соответственно.

Треугольник $AMN$ – равнобедренный, так как $AD$ – биссектриса и высота этого треугольника.

Тогда $AD$ – медиана треугольника $AMN$, то есть $MD=ND$.

Тогда треугольники $BMD$ и $CND$ равны по первому признаку $(\angle BDM=\angle CDN$ как вертикальные, $BD=DC, MD=ND)$.

Тогда $\angle 4=\angle 5$, и, следовательно, прямые $AB$ и $AC$ параллельны, что невозможно.