Чтобы из графика $y=f(x)$ построить график $y=f(ax)$ при $a>1$ , нужно сжать изначальный график в $a$ раз к оси $Oy$.

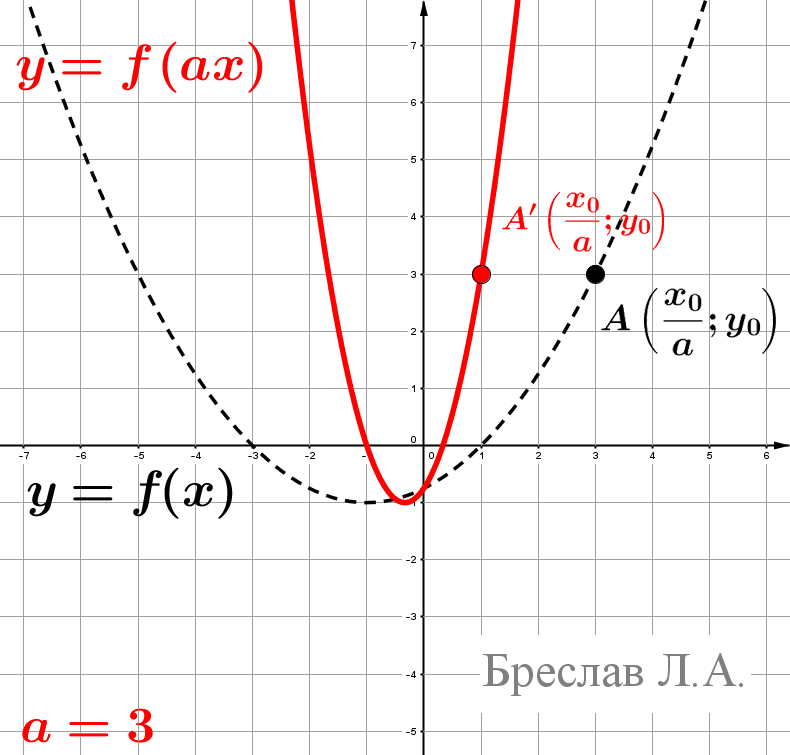Пусть точка $A(x_0;y_0)$ принадлежит графику $y=f(x)$, т.е. $y_0=f(x_0)$.

Тогда подстановкой легко проверить, что точка $A'\left(\dfrac{x_0}{a}; y_0\right)$ будет принадлежать графику $y=f(ax)$.

Действительно, $f\left(a\cdot\dfrac{x_0}{a}\right)=f(x_0)=y_0$.

Таким образом точка $A(x_0;y_0)$ перешла в точку $A'\left(\dfrac{x_0}{a}; y_0\right)$, которая лежит в $a$ раз ближе к оси $Oy$.

То есть модуль абсциссы точки уменьшился в $a$ раз, что соответствует сжатию графика в $a$ раз к оси $Oy$.

Чтобы из графика $y=f(x)$ построить график $y=f\left(\dfrac{1}{a}\cdot x\right)$ при $a>1$ , нужно растянуть изначальный график в $a$ раз от оси $Oy$.

Пусть точка $A(x_0;y_0)$ принадлежит графику $y=f(x)$, т.е. $y_0=f(x_0)$.

Тогда точка $A'\left(ax_0; y_0\right)$, которая лежит в $a$ раз дальше от оси $Oy$, будет принадлежать графику $y=f\left(\dfrac{1}{a}\cdot x\right)$.

Действительно, $f\left(\dfrac{1}{a}\cdot ax_0\right)=f(x_0)=y_0$.

Таким образом точка $A(x_0;y_0)$ перешла в точку $A'\left(ax_0; y_0\right)$.

То есть модуль абсциссы точки увеличился в $a$ раз, что соответствует растяжению графика в $a$ от оси $Oy$.