Содержание
Теорема Фалеса
Если на одной из двух прямых отложить последовательно несколько равных отрезков, а потом через их концы провести параллельные прямые, то они отсекут на другой прямой равные отрезки.
Доказательство
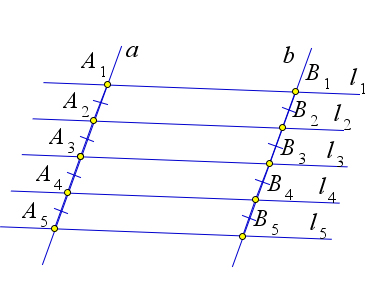
Пусть параллельные прямые $l_1, l_2, l_3$ пересекают прямые $a$ и $b$ в точках $A_1, A_2, A_3$ и $B_1, B_2, B_3$ соответственно.
Пусть при этом $A_1A_2=A_2A_3$.
Докажем, что тогда $B_1B_2=B_2B_3$.
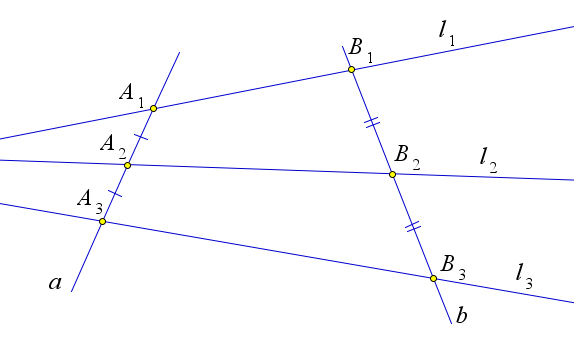
Рассмотрим случай, когда прямые a и b параллельны.
Тогда $A_2A_1B_1B_2$ и $A_3A_2B_2B_3$ – параллелограммы.
Следовательно, $A_1A_2=B_1B2$ и $A_2A_3=B_2B_3$, и так как $A_1A_2=A_2A_3$, то $B_1B_2=B_2B_3$.
Рассмотрим случай, когда прямые a и b не параллельны.
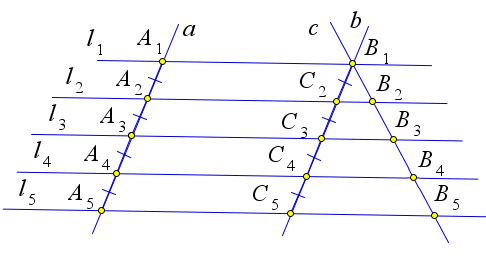
Проведем через точку $B_1$ прямую $c$, параллельную прямой $a$.
Пусть прямые $l_2,l_3,l_4$ и прямая $c$ пересекаются в точках $C_2, C_3, C_4$.
По первому случаю $B_1C_2=C_2C_3$, кроме того $B_2C_2\parallel B_3C_3$.
Тогда $B_2C_2$ – средняя линия $\triangle B_1C_3B_3$, то есть $B_1B_2=B_2B_3$.
Замечание
Утверждение обратное теореме Фалеса неверно.
То есть, из того, что прямые прямые $l_1, l_2, l_3$ пересекают прямые $a$ и $b$ в точках $A_1, A_2, A_3$ и $B_1, B_2, B_3$ соответственно, и при этом $A_1A_2=A_2A_3$ и $B_1B_2=B_2B_3$, не следует, что прямые $l_1, l_2$ и $l_3$ параллельны.
