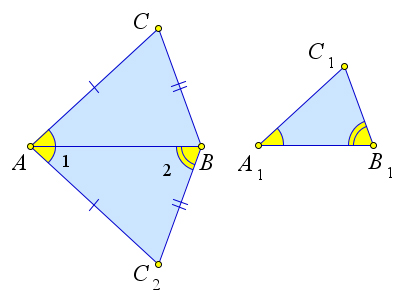
Третий признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
Доказательство
Первый способ (не использует тригонометрию)
Пусть стороны треугольников $ABC$ и $A_1B_1C_1$ пропорциональны:
$\dfrac{AB}{A_1B_1}=\dfrac{BC}{B_1C_1}=\dfrac{CA}{C_1A_1}$.
Докажем, что $\triangle ABC\sim \triangle A_1B_1C_1$.
Для этого, учитывая второй признак подобия треугольников, достаточно доказать, что $\angle
A=\angle A_1$. Рассмотрим треугольник $ABC_2$, у которого $\angle 1=\angle A_1,
\angle 2=\angle B_1$.
Треугольники $ABC_2$ и $A_1B_1C_1$ подобны по первому признаку подобия треугольников, поэтому
$\dfrac{AB}{A_1B_1}=\dfrac{BC_2}{B_1C_1}=\dfrac{C_2A}{C_1A_1}$.
Сравнивая эти равенства с первой пропорцией подобия, получаем:
$BC=BC_2, CA=C_2A$.
Тогда треугольники $ABC$ и $ABC_2$ равны по трем
сторонам.
Отсюда следует, что $\angle A=\angle 1$, a так как $\angle 1=\angle A_1$, то $\angle A=\angle A_1$.
Второй способ (использует тригонометрию).
Рассмотрим треугольники $ABC$ и $A_1B_1C_1$ со сторонами $a, b, c$ и
$a_1, b_1, c_1$.
Докажем, что если $\dfrac{a}{a_1}=\dfrac{b}{b_1}=\dfrac{c}{c_1}$, то $\triangle ABC\sim\triangle A_1B_1C_1$.
Обозначим $k=\dfrac{a}{a_1}$.
Тогда $a=ka_1, b=kb_1, c=kc_1$.
По теореме косинусов имеем $$\cos{C}=\frac{a^2+b^2-c^2}{2ab}=\frac{k^2a_1^2+k^2b_1^2-k^2c_1^2}{2ka_1kb_1}=\frac{k^2(a_1^2+b_1^2-c_1^2)}{k^22a_1b_1}=\frac{a_1^2+b_1^2-c_1^2}{2a_1b_1}=\cos{C_1}.$$
следовательно, $\angle C=\angle C_1$.
Аналогично $\angle A=\angle A_1$ и $\angle B=\angle
B_1$.
То есть углы треугольников соответственно равны, а стороны пропорциональны, следовательно $\triangle ABC\sim\triangle A_1B_1C_1$.