Содержание
Координаты векторов
Определение
Линейной комбинацией векторов $\vec{a}$ и $\vec{b}$ называется вектор $\alpha \vec{a}+\beta \vec{b}$.
Числа $\alpha$ и $\beta$ называются коэффициентами линейной комбинации.
Лемма
Если вектора $\vec{a}$ и $\vec{b}$ неколлинеарны и $x\vec{a}+y\vec{b}=\vec{0}$, то $x=y=0$.
Доказательство
Предположим, что $x\neq0$. Тогда можно выразить $\vec{a}=-\frac{y}{x}\vec{b}$, откуда следует, что $\vec{a} \parallel \vec{b}$, что противоречит условию. Таким образом $x=0$. Аналогично можно доказать, что $y=0$.
Теорема о разложении вектора на составляющие
Любой вектор можно единственным образом представить в виде линейной комбинации двух наперед заданных неколлинеарных векторов.
Доказательство
Пусть $\vec{a}$ и $\vec{b}$ – данные неколлинеарные векторы.
Докажем, что любой вектор $\vec{p}$ можно разложить по векторам $\vec{a}$ и $\vec{b}$.
Возможны два случая.
Первый случай
Вектор $\vec{p}$ коллинеарен одному из векторов $\vec{a}$ и $\vec{b}$, например вектору $\vec{b}$.
В этом случае по теореме \ref{139} вектор $p$ можно представить в виде $\vec{p}=y\vec{b}$, где $y$ – некоторое число, и, следовательно, $\vec{p}=0\cdot \vec{a}+y\cdot \vec{b}$, то есть вектор $\vec{p}$ разложен по векторам $\vec{a}$ и $\vec{b}$.
Второй случай
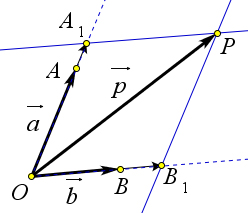
Вектор $\vec{p}$ не коллинеарен ни вектору $\vec{a}$, ни вектору $\vec{b}$.
Отметим какую-нибудь точку $O$ и отложим от неё векторы $\overrightarrow{OA}=\vec{a}, \overrightarrow{OB}=\vec{b}, \overrightarrow{OP}=\vec{p}$.
Через точку $P$ проведём прямую, параллельную прямой $OB$, и обозначим через $A_1$ точку пересечения этой прямой с прямой $OA$.
По правилу треугольника $\vec{p}=\overrightarrow{OA_1}+\overrightarrow{A_1P}$. Но векторы $\overrightarrow{OA_1}$ и $\overrightarrow{A_1P}$ коллинеарны соответственно векторам $\vec{a}$ и $\vec{b}$, поэтому существуют числа $x$ и $y$, такие, что $\overrightarrow{OA_1}=x\vec{a}, \overrightarrow{A_1P}=y\vec{b}$.
Следовательно, $\vec{p}=x\vec{a}+y\vec{b}$, то есть вектор $\vec{p}$ разложен по векторам $\vec{a}$ и $\vec{b}$.
Докажем теперь, что коэффициенты $x$ и $y$ разложения определяются единственным образом.
Допустим, что наряду с разложением $\vec{p}=x\vec{a}+y\vec{b}$ имеет место разложение $\vec{p}=x_1\vec{a}+y_1\vec{b}$.
Вычитая второе равенство из первого и используя правила действий над векторами, получаем $\vec{0}=(x-x_1)\vec{a}+(y-y_1)\vec{b}$.
Но это равенство может выполняться, только если $x-x_1=y-y_1=0$.
В самом деле, если предположить, что например $x-x_1\neq0$, то из полученного равенства найдем $\vec{a}=-\frac{y-y_1}{x-x_1}\vec{b}$, а значит, векторы $\vec{a}$ и $\vec{b}$ коллинеарны.
Но это противоречит условию теоремы.
Следовательно, $x-x_1=0$ и $y-y_1=0$.
Откуда $x=x_1$ и $y=y_1$.
Это и означает, что коэффициенты разложения вектора $\vec{p}$ определяются единственным образом.
Определение
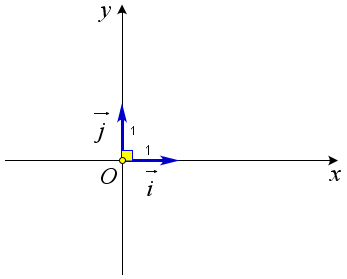
Пусть прямая $Oy \parallel\vec{j}$, а прямая $Ox \parallel\vec{i}$, кроме того $Oy\perp Ox$, и $\vec{i}\perp\vec{j}$, $|\vec{i}|=|\vec{j}|=1$ (рис. \ref{pic142}).
Тогда говорят, что на плоскости $xOy$ задана прямоугольная система координат, а коэффициенты разложения произвольного вектора $\vec{a}$ по базису $(\vec{i},\vec{j})$ называются координатами вектора $\vec{a}$ в этой системе координат. То есть, если $\vec{a}=a_x\vec{i}+a_y\vec{j}$, то говорят, что вектор $\vec{a}$ имеет координаты $(a_x, a_y)$.
Вектора $\vec{i}$ и $\vec{j}$ называют координатными ортами.
Теорема
Если вектор $\vec{a}$ в системе координат $xOy$ имеет координаты $(a_x, a_y)$, то числа $a_x$ и $a_y$ совпадают с проекциями вектора $\vec{a}$ на координатные оси $Ox$ и $Oy$ соответственно, то есть $a_x=pr_{Ox}{\vec{a}}$ и $a_y=pr_{Oy}{\vec{a}}$.
Определение
Теорема
- Два вектора равны тогда и только тогда, когда их координаты соответственно равны.
- При сложении векторов их соответствующие координаты складываются.
- При умножении вектора на число его координаты умножаются на это число.
Доказательство
Первое
Пусть $\vec{a}=\vec{b}$, $\vec{a}=x\vec{i}+y\vec{j}, \vec{b}=x_1\vec{i}+y_1\vec{j}$.
Тогда $x\vec{i}+y\vec{j}=x_1\vec{i}+y_1\vec{j}$ или $(x-x_1)\vec{i}+(y-y_1)\vec{j}=0$. Так как $\vec{i}\not \parallel \vec{j}$, то по лемме \ref{lmm-lin-nezavisimost} $x-x_1=y-y_1=0$, то есть $x=x_1$ и $y=y_1$.
Обратно, если $\vec{a}=x\vec{i}+y\vec{j}$, и $\vec{b}=x\vec{i}+y\vec{j}$, то очевидно $\vec{a}=\vec{b}$.
Второе
Рассмотрим вектора $\vec{a}(x_1; y_1)$ и $\vec{b}(x_2; y_2)$.
Так как $\vec{a}=x_1\vec{i}+y_1\vec{j}$ и $\vec{b}=x_2\vec{i}+y_2\vec{j}$ то, пользуясь свойствами сложения векторов и умножения вектора на число, получим: $\vec{a}+\vec{b}=x_1\vec{i}+y_1\vec{j}+x_2\vec{i}+y_2\vec{j}=(x_1+x_2)\vec{i}+(y_1+y_2)\vec{j}$.
Отсюда следует, что координаты вектора $\vec{a}+\vec{b}$ равны $(x_1+x_2; y_1+y_2)$.
Третье
Пусть вектор $\vec{a}$ имеет координаты $(x;y)$.
Тогда вектор $k\vec{a}=k(x\vec{i}+y\vec{j})=kx\vec{i}+ky\vec{j}$, то есть координаты вектора $k\vec{a}$ равны $(kx;ky)$.
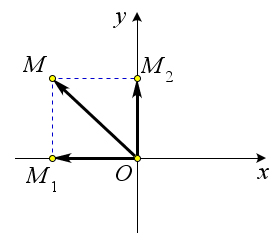
Теорема
Доказательство
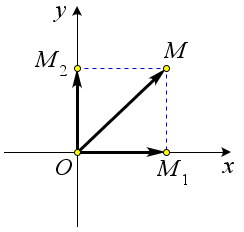
Пусть $\overrightarrow{OM}=\overrightarrow{OM_1}+\overrightarrow{OM_2}$.
Докажем, что $\overrightarrow{OM_1}=x\vec{i}$ и $\overrightarrow{OM_2}=y\vec{j}$.
В самом деле, если $x>0$, то $x=|OM_1|$, а векторы $\overrightarrow{OM_1}$ и $\vec{i}$ сонаправлены.
Поэтому $\overrightarrow{OM_1}=|OM_1|\cdot \vec{i}=x\vec{i}$.
Если $x<0$, то $x=-|OM_1|$, а векторы $\overrightarrow{OM_1}$ и $\vec{i}$ противоположно направлены.
Поэтому $\overrightarrow{OM_1}=-|OM_1|\vec{i}=x\vec{i}$.
Наконец, если $x=0$, то $\overrightarrow{OM_1}=\vec{0}$ и равенство $\overrightarrow{OM_1}=x\vec{i}$ в этом случае также справедливо.
Таким образом, в любом случае $\overrightarrow{OM_1}=x\vec{i}$.
Аналогично доказывается, что $\overrightarrow{OM_2}=y\vec{j}$.
Следовательно, $\overrightarrow{OM}=\overrightarrow{OM_1}+\overrightarrow{OM_2}=x\vec{i}+y\vec{j}$.
Отсюда следует, что координаты радиус-вектора $\overrightarrow{OM}$ равны $(x;y)$, то есть равны соответствующим координатам точки $M$.
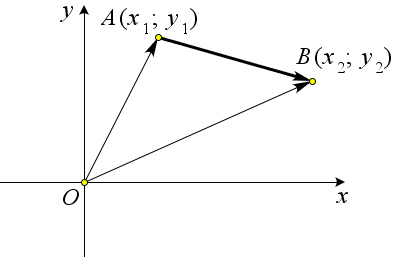
Связь координат вектора и координат его начала и конца
Доказательство
Пусть точка $A$ имеет координаты $(x_1;y_1)$, а точка $B$ имеет координаты $(x_2;y_2)$.
Тогда $\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=(x_2;y_2)-(x_1;y_1)=(x_2-x_1; y_2-y_1)$.
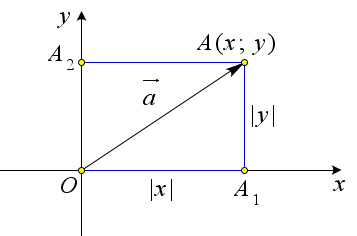
Теорема о модуле вектора
Для любого вектора $\vec{a}(x_1;y_1)$ его модуль вычисляется по формуле $|\vec{a}|=\sqrt{x_1^2+y_1^2}$.
Доказательство
Если $x=0$ или $y=0$, то формула очевидна.
Пусть $x\neq0$ и $y\neq0$.
Отложим от начала координат вектор $\overrightarrow{OA}=\vec{a}$ и проведем через точку $A$ перпендикуляры $AA_1$ и $AA_2$ к осям $Ox$ и $Oy$.
Координаты точки $A$ равны координатам вектора $\overrightarrow{OA}$, то есть $(x;y)$. Поэтому $|OA_1|=|x|, |AA_1|=|OA_2|=|y|$.
По теореме Пифагора $|OA|=\sqrt{|OA_1|^2+|AA_1|^2}=\sqrt{x^2+y^2}$.
Таким образом $|\vec{a}|=\sqrt{x^2+y^2}$.
Формула расстояния между двумя точками
Если $A(x_1;y_1)$ и $B(x_2;y_2)$, то $|AB|=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$ .
Доказательство
Если $A(x_1;y_1)$ и $B(x_2;y_2)$, то вектор $\overrightarrow{AB}$ имеет координаты $(x_2-x_1; y_2-y_1)$.
Следовательно, $|AB|=|\overrightarrow{AB}|=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$.
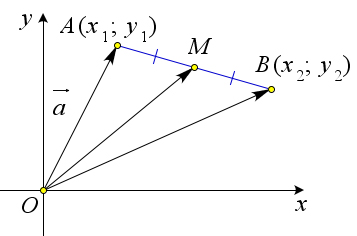
Координаты середины отрезка
Если $A(x_1;y_1)$ и $B(x_2;y_2)$, то точка $M$ середина отрезка $AB$ имеет координаты $M\left(\dfrac{x_1+x_2}{2};\dfrac{y_1+y_2}{2}\right)$.
Доказательство
По теореме $\overrightarrow{OM}=\frac{1}{2}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}$.
Таким образом $\displaystyle\overrightarrow{OM}=\frac{\overrightarrow{OA}+\overrightarrow{OB}}{2}=\frac{(x_1;y_1)+(x_2;y_2)}{2}=\frac{(x_1+x_2;y_1+y_2)}{2}=\left(\frac{x_1+x_2}{2};\frac{y_1+y_2}{2}\right)$.
Таким образом точка $M$ имеет координаты $\displaystyle\left(\frac{x_1+x_2}{2};\frac{y_1+y_2}{2}\right)$.
Координаты точки, разбивающий отрезок в данном отношении
…