Содержание
Определение
Определим отношение направленных отрезков следующим
образом:
- $\dfrac{\overrightarrow{AB}}{\overrightarrow{CD}}=\dfrac{|AB|}{|CD|}$, если векторы $\overrightarrow{AB}$ и $\overrightarrow{CD}$ сонаправленные.
- $\dfrac{\overrightarrow{AB}}{\overrightarrow{CD}}=-\dfrac{|AB|}{|CD|}$, если векторы $\overrightarrow{AB}$ и $\overrightarrow{CD}$ противонаправленные.
Замечание
Из определения следуют свойства:
- Можно менять знак: $\dfrac{\overrightarrow{AB}}{\overrightarrow{CD}}=-\dfrac{\overrightarrow{AB}}{\overrightarrow{DC}}$
- Можно «сокращать»: $\dfrac{\overrightarrow{AB}}{\overrightarrow{CD}}\cdot \dfrac{\overrightarrow{CD}}{\overrightarrow{EF}}=\dfrac{\overrightarrow{AB}}{\overrightarrow{EF}}$
- Можно делить обе части равенства на отношение: если $\dfrac{\overrightarrow{AB}}{\overrightarrow{CD}}=\dfrac{\overrightarrow{EF}}{\overrightarrow{KL}}$, то $\dfrac{\overrightarrow{AB}}{\overrightarrow{CD}}\cdot\dfrac{\overrightarrow{KL}}{\overrightarrow{EF}}=1$
Теорема Менелая
Точки $A_1,B_1$ и $C_1$, лежащие на сторонах треугольника $ABC$ или
на их продолжениях, лежат на одной прямой тогда и только тогда,
когда
$\dfrac{\overrightarrow{AC_1}}{\overrightarrow{C_1B}}\cdot\dfrac{\overrightarrow{BA_1}}{\overrightarrow{A_1C}}\cdot\dfrac{\overrightarrow{CB_1}}{\overrightarrow{B_1A}}=-1$.
Доказательство
Докажем прямую теорему
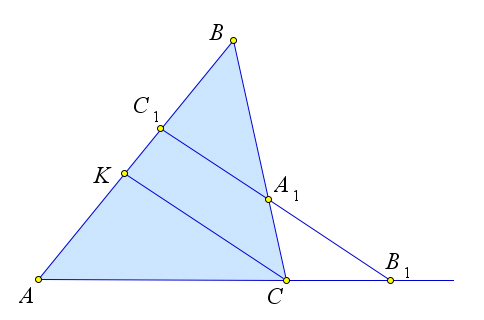
Рассмотрим треугольник $ABC$, и пусть прямая $l$ пересекает стороны
$AB, BC, CA$ или их продолжения в точках $C_1, A_1$ и $B_1$
соответственно.
Докажем, что тогда
$\dfrac{\overrightarrow{AC_1}}{\overrightarrow{C_1B}}\cdot\dfrac{\overrightarrow{BA_1}}{\overrightarrow{A_1C}}\cdot\dfrac{\overrightarrow{CB_1}}{\overrightarrow{B_1A}}=-1$.
Проведем через вершину $C$ прямую $p$, параллельную прямой $l$.
Пусть $K$ – это точка пересечения прямых $p$ и $AC$.
По теореме Фалеса
$\dfrac{\overrightarrow{AB_1}}{\overrightarrow{B_1C}}=\dfrac{\overrightarrow{AC_1}}{\overrightarrow{C_1K}},
\dfrac{\overrightarrow{CA_1}}{\overrightarrow{A_1B}}=-\dfrac{\overrightarrow{C_1K}}{\overrightarrow{C_1B}}$.
Перемножив эти равенства, получим $\dfrac{\overrightarrow{AB_1}\cdot
\overrightarrow{CA_1}}{\overrightarrow{B_1C}\cdot
\overrightarrow{A_1B}}=-\dfrac{\overrightarrow{AC_1}}{\overrightarrow{C_1B}}$,
откуда следует, что
$\dfrac{\overrightarrow{AC_1}}{\overrightarrow{C_1B}}\cdot\dfrac{\overrightarrow{BA_1}}{\overrightarrow{A_1C}}\cdot\dfrac{\overrightarrow{CB_1}}{\overrightarrow{B_1A}}=-1$.
Докажем обратную теорему.
Рассмотрим треугольник $ABC$. Пусть на
прямых $AB, BC$ и $AC$ выбраны точки $C_1, A_1$ и $B_1$
соответственно.
Докажем, что если
$\dfrac{\overrightarrow{AC_1}}{\overrightarrow{C_1B}}\cdot\dfrac{\overrightarrow{BA_1}}{\overrightarrow{A_1C}}\cdot\dfrac{\overrightarrow{CB_1}}{\overrightarrow{B_1A}}=-1$,
то точки $A_1, B_1$ и $C_1$ лежат на одной прямой.
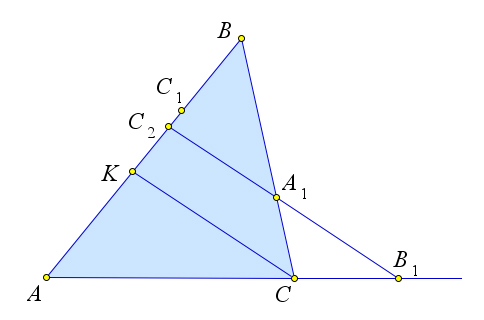
Пусть прямая $A_1B_1$ пересекает прямую $AB$ в точке $C_2$.
Докажем, что $C_2=C_1$.
Действительно, так как точки $A_1,
B_1$ и $C_2$ лежат на одной прямой, то для них выполняется равенство
$\dfrac{\overrightarrow{AC_2}}{\overrightarrow{C_2B}}\cdot\dfrac{\overrightarrow{BA_1}}{\overrightarrow{A_1C}}\cdot\dfrac{\overrightarrow{CB_1}}{\overrightarrow{B_1A}}=-1$.
Но тогда $\dfrac{\overrightarrow{AC_2}}{\overrightarrow{C_2B}}=-\dfrac{\overrightarrow{A_1C}}{\overrightarrow{BA_1}}\cdot\dfrac{\overrightarrow{B_1A}}{\overrightarrow{CB_1}}=\dfrac{\overrightarrow{AC_1}}{\overrightarrow{C_1B}}$, что и означает, что $C_1=C_2$.
Замечание
Картинка может отличаться от той, что дана при доказательстве теоремы. Но все рассуждения останутся верны. (Нужен рисунок)
Следствие
Теорема Менелая в скалярной форме.
Следствие (теорема о двух чевианах)
Пусть в треугольнике $ABC$ чевианы $AA_1$ и $BB_1$ пересекаются в точке $O$. Тогда $\dfrac{AO}{OA_1}=\dfrac{AB_1}{B_1C}\left(\dfrac{CA_1}{A_1B}+1\right)$.
