Содержание
Теорема 1
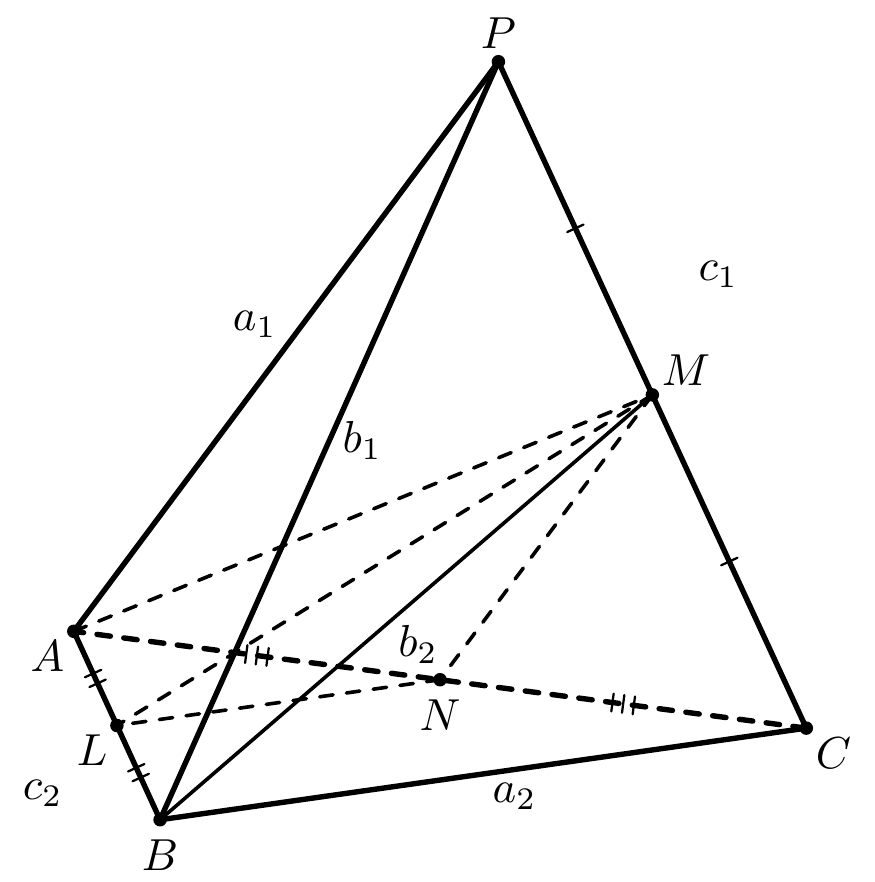
Рассмотрим тетраэдр $PABC$, в котором $PA = a_1, BC = a_2, PB = b_1, AC = b_2, PC = c_1, AB = c_2$. Угол между ребрами $PA$ и $BC$ обозначим $\varphi$. Тогда $\varphi$ можно вычислить по формуле: $$\varphi = \arccos{\dfrac{|c_1^2+c_2^2-b_1^2-b_2^2|}{2\cdot a_1\cdot a_2}}.$$
Доказательство
Построим отрезки $MN$ и $NL$ – средние линии треугольников $APC$ и $ABC$. Тогда, в силу параллельности, $\varphi=\angle(MN, NL)$.
Найдем угол $\angle LNM$. Для этого найдем все стороны треугольника $LNM$.
$LN = \dfrac{a_2}{2} , MN = \dfrac{a_1}{2}$, так как это средние линии.
Отрезок $LM$ – это медиана треугольника $AMB$. Отрезки $AM$ и $BM$, в свою очередь, являются медианами треугольников $APC$ и $BPC$ соответственно. Тогда, применяя формулу для нахождения медианы, получаем: $AM = \dfrac{1}{2}\sqrt{2a_1^2+2b_2^2-c_1^2}, BM = \dfrac{1}{2}\sqrt{2b_1^2+2a_2^2-c_1^2}$
Используем эти соотношения для нахождения $LM$ по той же формуле: $LM = \dfrac{1}{2}\sqrt{2AM^2+2BM^2-AB^2}=\\ = \dfrac{1}{2}\sqrt{2\cdot\dfrac{1}{4}(2a_1^2+2b_2^2-c_1^2)+2\cdot\dfrac{1}{4}(2b_1^2+2a_2^2-c_1^2)-c_2^2}=\\=\dfrac{1}{2}\sqrt{a_1^2+a_2^2+b_1^2+b_2^2-c_1^2-c_2^2}$.
Теперь нам известны все стороны в треугольнике $LMN$. Тогда, по теореме косинусов: $\cos{\angle LNM} = \dfrac{LN^2+MN^2-LM^2}{2\cdot LN\cdot MN} =\\=\dfrac{\dfrac{a_2^2}{4}+\dfrac{a_1^2}{4}-\dfrac{1}{4}(a_1^2+a_2^2+b_1^2+b_2^2-c_1^2-c_2^2)}{2\cdot\dfrac{a_1\cdot a_2}{4}} =\\= \dfrac{c_1^2+c_2^2-b_1^2-b_2^2}{2\cdot a_1\cdot a_2}$.
Искомый угол $\varphi$ является углом между прямыми, а значит, $\varphi \leqslant 90^\circ$. Кроме того, либо $\varphi=\angle LNM$, либо $\varphi=180^\circ-\angle LNM$. Из этого следует, что $cos{\varphi}=|\cos{\angle LNM}|$. А значит, $$\varphi = \arccos{\dfrac{|c_1^2+c_2^2-b_1^2-b_2^2|}{2\cdot a_1\cdot a_2}}.$$
Теорема 2
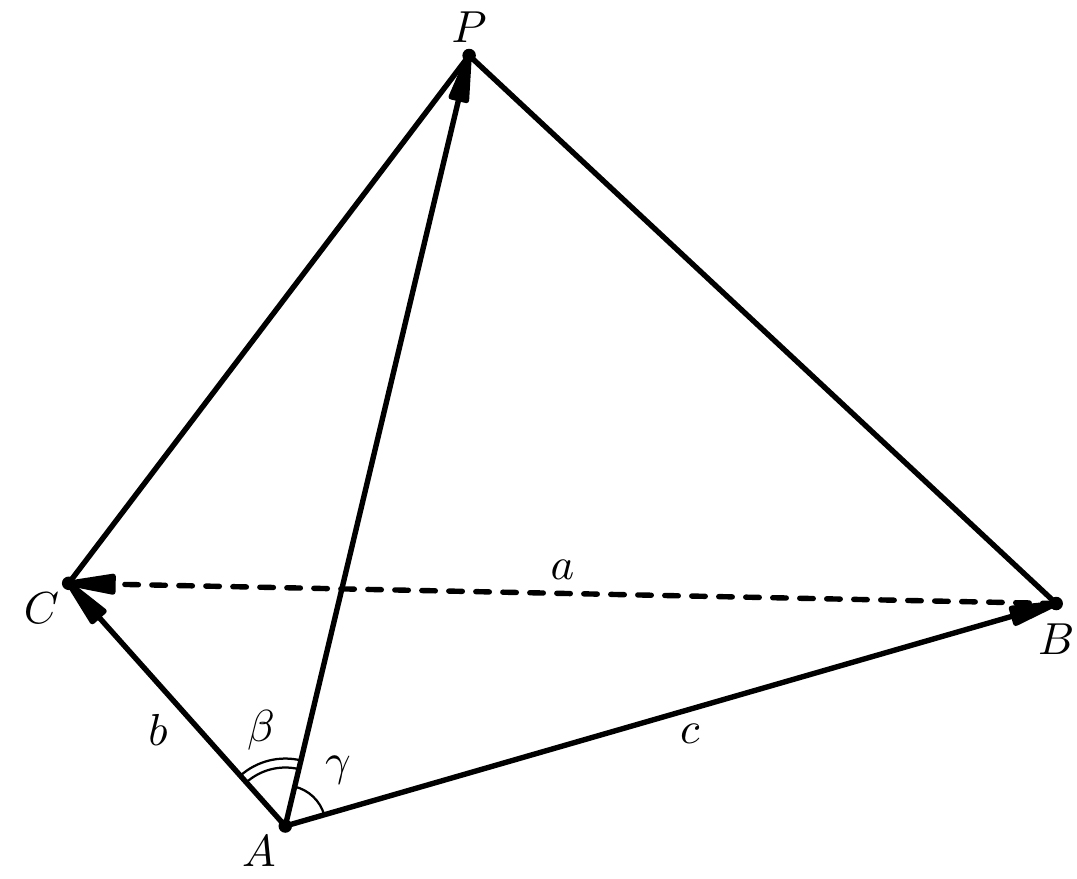
Рассмотрим тетраэдр $PABC$, в котором $BC = a, AC = b, AB = c, \angle PAC = \beta, \angle PAB = \gamma$. Угол между ребрами $PA$ и $BC$ обозначим $\varphi$. Тогда $\varphi$ можно вычислить по формуле: $$\varphi = \arccos{\dfrac{|b\cdot\cos{\beta}-c\cdot\cos{\gamma}|}{a}}.$$
Доказательство
Выпишем скалярное произведение векторов $\overrightarrow{AP}$ и $\overrightarrow{BC}$:
$\overrightarrow{AP}\cdot\overrightarrow{BC}=|AP|\cdot |BC|\cdot\cos{\angle(\overrightarrow{AP},\overrightarrow{BC})}$.
Тогда $\cos{\angle(\overrightarrow{AP},\overrightarrow{BC})} = \dfrac{\overrightarrow{AP}\cdot\overrightarrow{BC}}{|AP|\cdot|BC|}$.
Заметим, что $\overrightarrow{BC} = \overrightarrow{AC}-\overrightarrow{AB}$. Подставим это соотношение в формулу для косинуса и раскроем скобки в числителе:
$\cos{\angle(\overrightarrow{AP},\overrightarrow{BC})} = \dfrac{\overrightarrow{AP}\cdot\overrightarrow{BC}}{|AP|\cdot|BC|}=\\=\dfrac{\overrightarrow{AP}\cdot(\overrightarrow{AC}-\overrightarrow{AB})}{|AP|\cdot|BC|}=\dfrac{\overrightarrow{AP}\cdot\overrightarrow{AC}-\overrightarrow{AP}\cdot\overrightarrow{AB}}{|AP|\cdot|BC|} = \\ = \dfrac{|AP|\cdot|AC|\cdot\cos{\beta}-|AP|\cdot|AB|\cdot\cos{\gamma}}{|AP|\cdot|BC|}=\\=\dfrac{|AC|\cdot\cos{\beta}-|AB|\cdot\cos{\gamma}}{|BC|}.$
Искомый угол $\varphi$ является углом между прямыми, а значит, $\varphi \leqslant 90^\circ$. Кроме того, $\varphi=\angle(\overrightarrow{AP},\overrightarrow{BC})$, либо $\varphi=180^\circ-\angle(\overrightarrow{AP},\overrightarrow{BC})$. Из этого следует, что $cos{\varphi}=|\cos{\angle(\overrightarrow{AP},\overrightarrow{BC})}|$.
Подставив обозначения из условия, получим формулу: $$\varphi = \arccos{\dfrac{|b\cdot\cos{\beta}-c\cdot\cos{\gamma}|}{a}}.$$