math-public:metodraspolozheniyaparabol_breslav_l_a
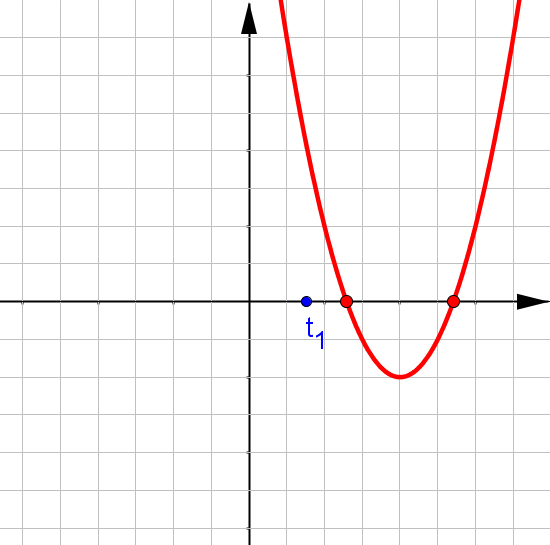
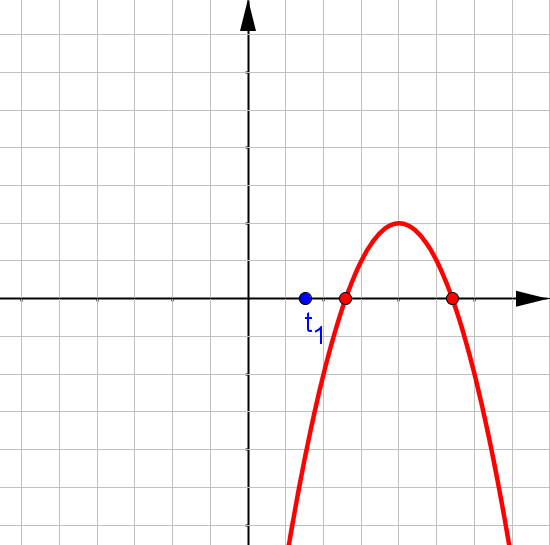
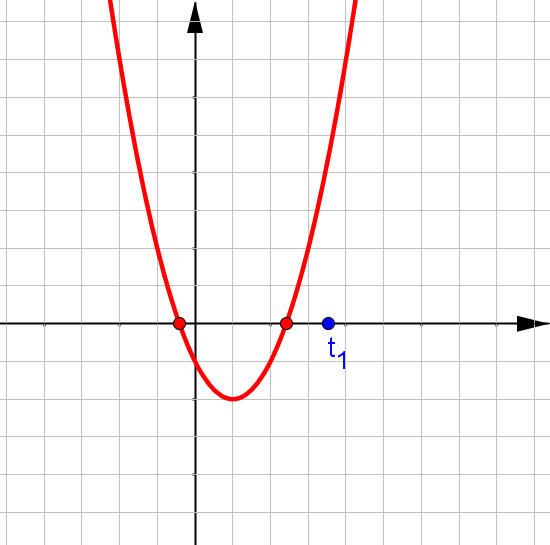
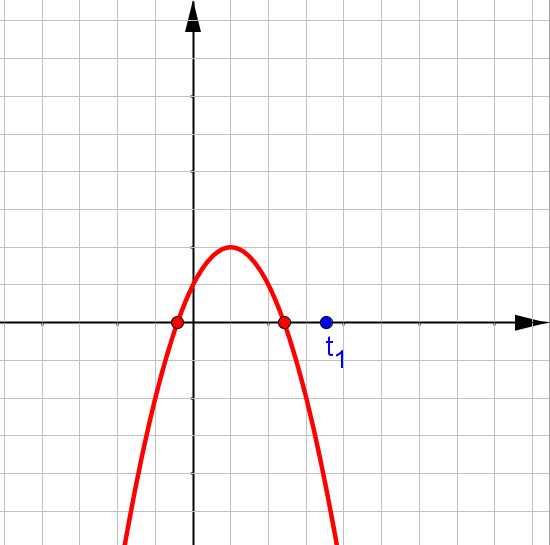
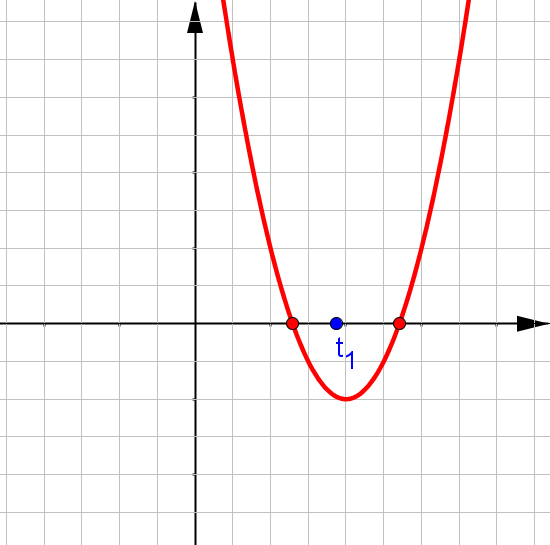
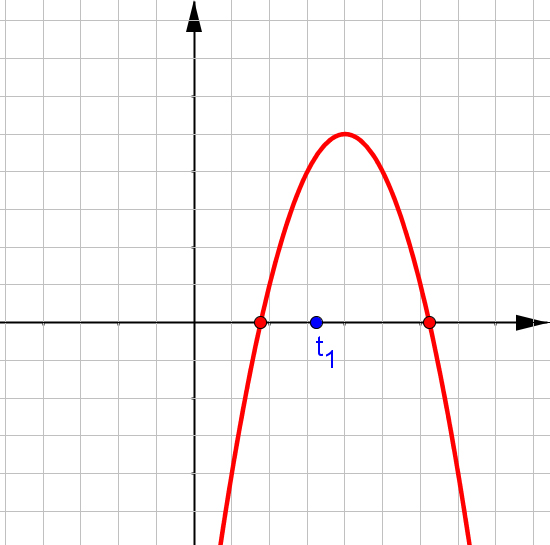
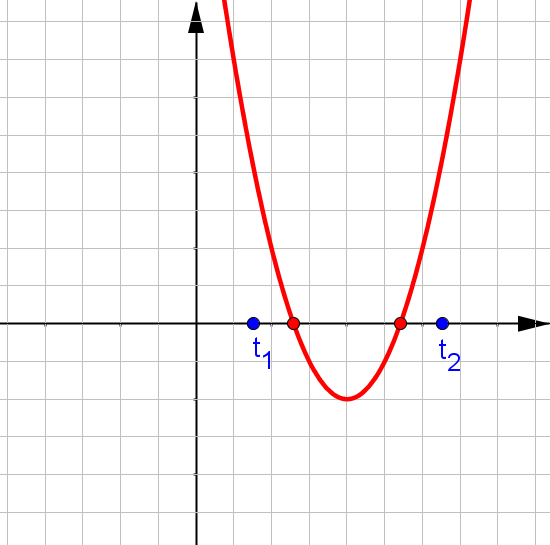
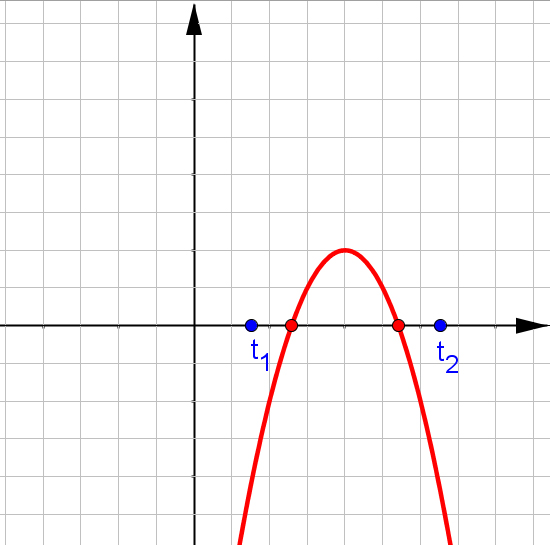
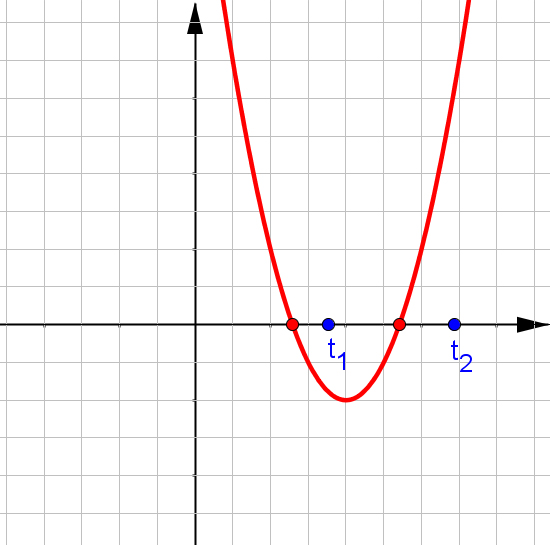
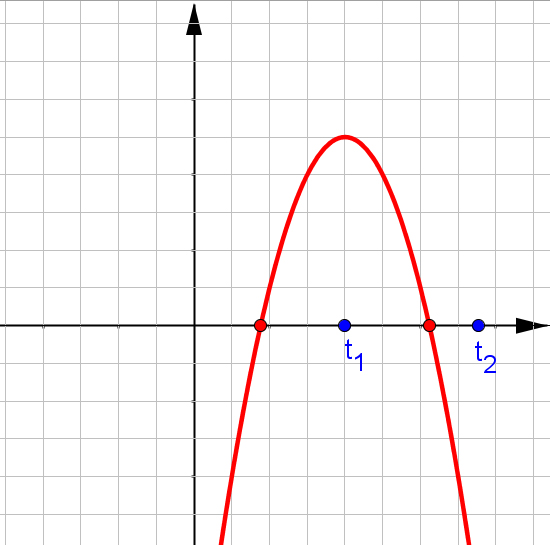
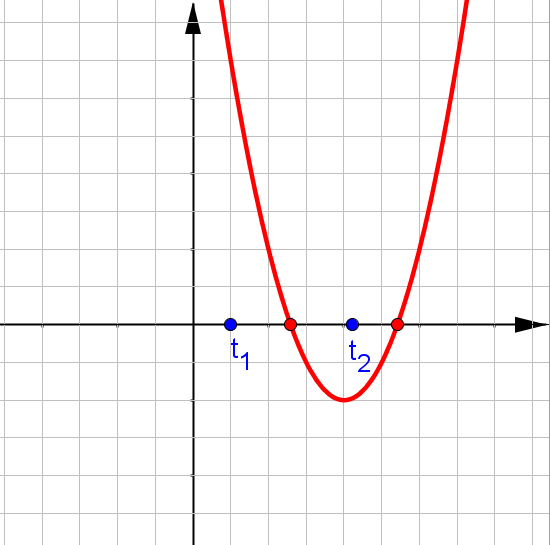
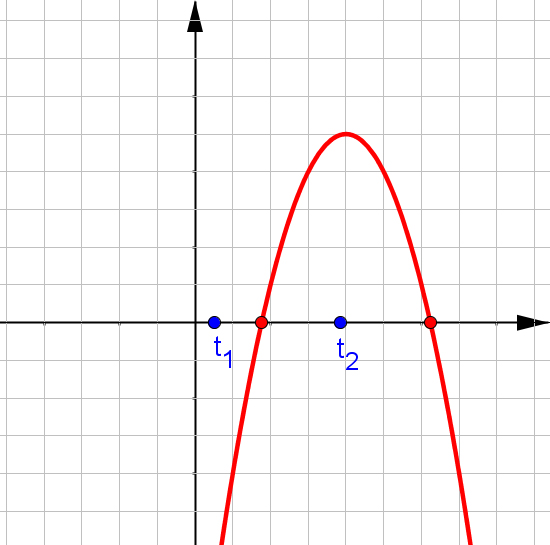
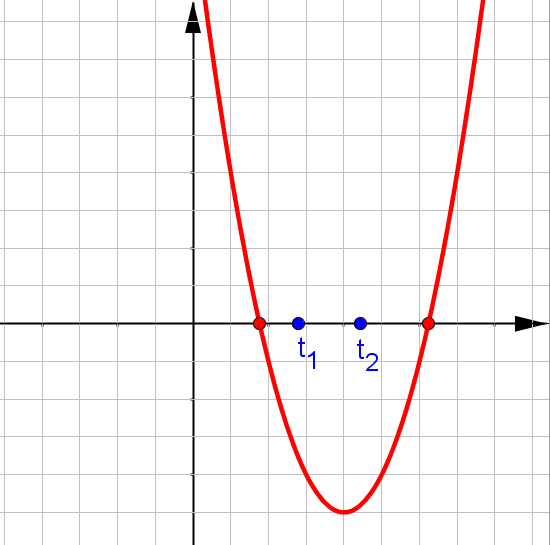
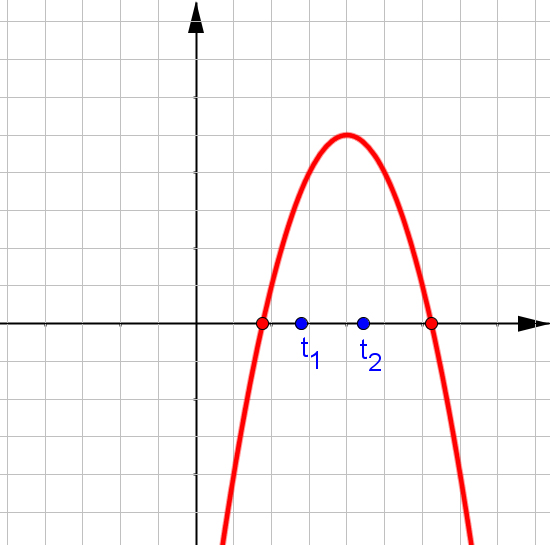
$f(x)=ax^2+bx+c$, при $a\neq0$.
Случаи с нестрогими неравенствами:
Комбинированные условия:
math-public/metodraspolozheniyaparabol_breslav_l_a.txt · Последнее изменение: — labreslav