Содержание
Общее определение
- Косинус острого угла равен отношению проекции к наклонной.
- Косинус тупого угла равен косинусу смежного с ним угла, взятого с другим знаком.
- Косинус прямого угла равен нулю.
- Косинус развернутого угла равен минус единице.
Корректность определения косинуса
Значение косинуса угла не зависит от того, какую длину наклонной выбрать.
Доказательство
Первый способ.
Следует из корректности определения синуса и теоремы Пифагора.
Второй способ.
Следует из подобия треугольников.
Свойства косинуса
- Косинус любого угла не больше $1$ и не меньше $-1$.
- $\cos{(180^\circ-\alpha)}=-\cos{\alpha}$.
- При возрастании угла от $0^\circ$ до $180^\circ$ косинус убывает от 1 до -1.
- Косинус однозначно определяет угол.
Доказательство
Докажем первый пункт теоремы.
Первое свойство следует из того, что проекция меньше наклонной.
Докажем второй пункт теоремы.
Второе свойство следует из того, что углы $180^\circ-\alpha$ и $\alpha$ являются смежными.
Докажем третий пункт теоремы.
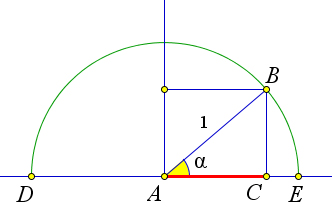
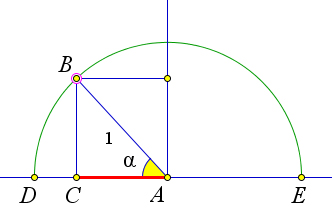
Рассмотрим окружность единичного радиуса с центром в точке $A$ и диаметром $DE$.
Пусть на прямой $DE$ задана числовая ось с началом в точке $A$ и единичным отрезком $AE$.
Проведем радиус $AB$ и получим угол $\a BAE$ некоторой величины $\alpha$.
Пусть точка $C$ является проекцией точки $B$ на прямую $DE$.
Тогда $\cos{\alpha}=AC$ при $\alpha\leqslant 90^\circ$ и $\cos{\alpha}=-AC$ при $\alpha>90^\circ$.
Это означает, что $\cos{\alpha}$ равен координате точки $C$ на оси $AE$.
Когда $\alpha$ возрастает $0^\circ$ до $180^\circ$ (то есть, когда точка $B$ пробегает полуокружность от точки $E$ до точки $D$), точка $C$ пробегает диаметр $ED$ от точки $E$ до точки $D$.
При этом координата точки $C$, то есть $\cos{\alpha}$, убывает от $1$ до $-1$.
Докажем четвертый пункт теоремы.
Пусть $\cos{\alpha}=\cos{\beta}$.
Докажем, что тогда $\alpha=\beta$.
Действительно, возможно три случая:
- $\alpha>\beta$. Тогда по пункту 3 $\cos{\alpha}<\cos{\beta}$. Значит, этот случай не имеет места.
- $\alpha<\beta$. Тогда по пункту 3 $\cos{\alpha}>\cos{\beta}$. Значит, этот случай не имеет места.
- Следовательно, остаётся только третья возможность: $\alpha=\beta$.