math-public:vectmetodkratko
| Нормаль к плоскости | Смешанное произведение векторов | Векторное произведение |
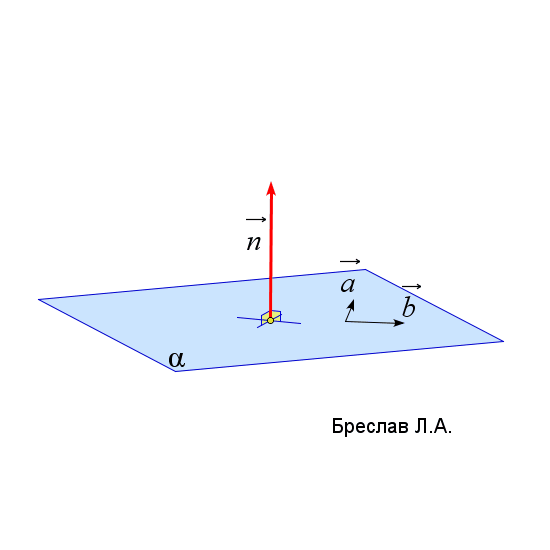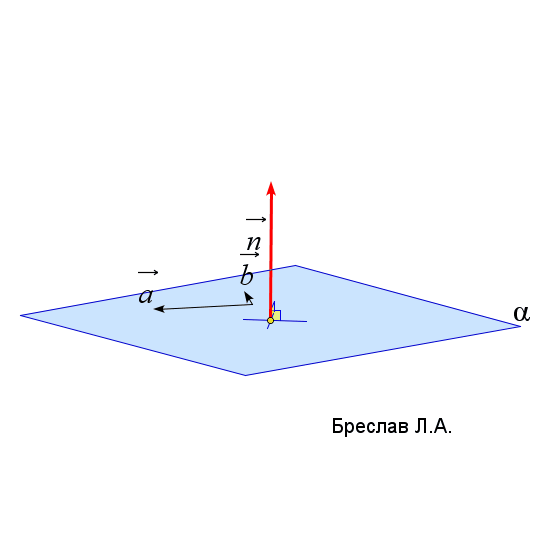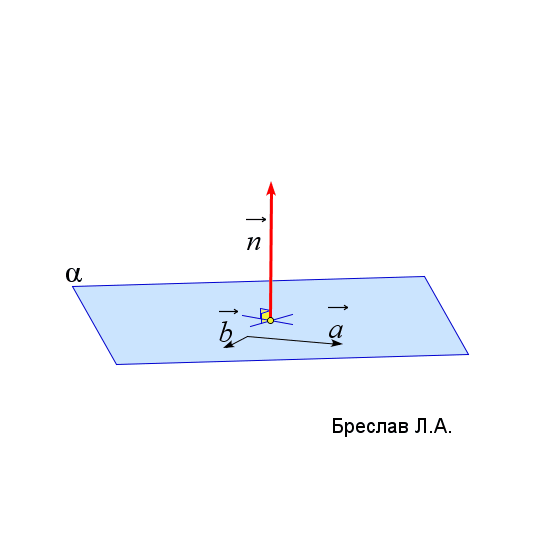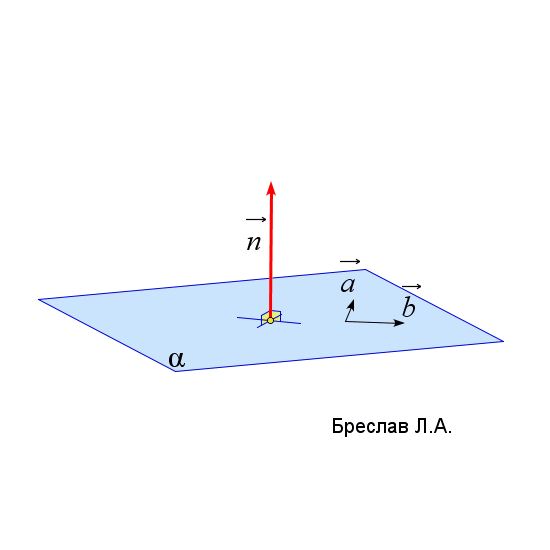 |  |  |
$\vec{n}_\alpha=\left|\begin{array}{ccc} \vec{i}&\vec{j}&\vec{k}\\ a_x&a_y&a_z\\ b_x&b_y&b_z\end{array}\right|$
$\vec{a}$ и $\vec{b}$ лежат в плоскости $\alpha$
$\vec{a}=(a_x;a_y;a_z), \vec{b}=(b_x;b_y;b_z)$ | $(\vec{a},\vec{b},\vec{c})=\left|\begin{array}{ccc} a_x&a_y&a_z\\ b_x&b_y&b_z\\ c_x&c_y&c_z\end{array}\right|$
$\vec{a}=(a_x;a_y;a_z), \vec{b}=(b_x;b_y;b_z), \vec{c}=(c_x;c_y;c_z)$ | $\vec{a}\times\vec{b}=\left|\begin{array}{ccc} \vec{i}&\vec{j}&\vec{k}\\ a_x&a_y&a_z\\ b_x&b_y&b_z\end{array}\right|$
$\vec{a}=(a_x;a_y;a_z), \vec{b}=(b_x;b_y;b_z)$ |
Углы
| Угол между двумя прямыми | Угол между прямой и плоскостью | Угол между двумя плоскостями |
 |  |  |
$\angle (l_1;l_2)=\angle(\vec{a}, \vec{b})$
(оба угла должны быть острыми)
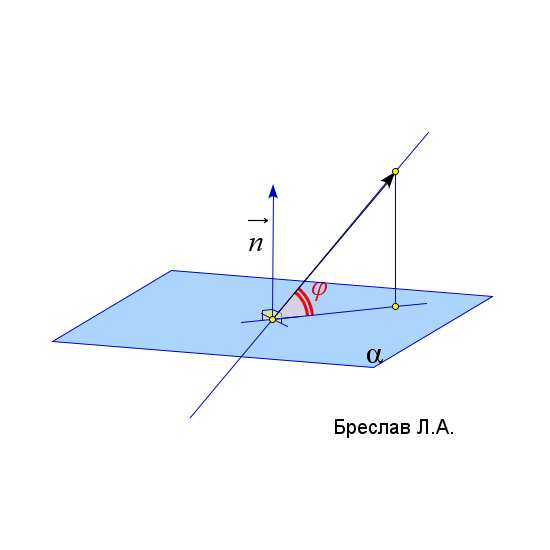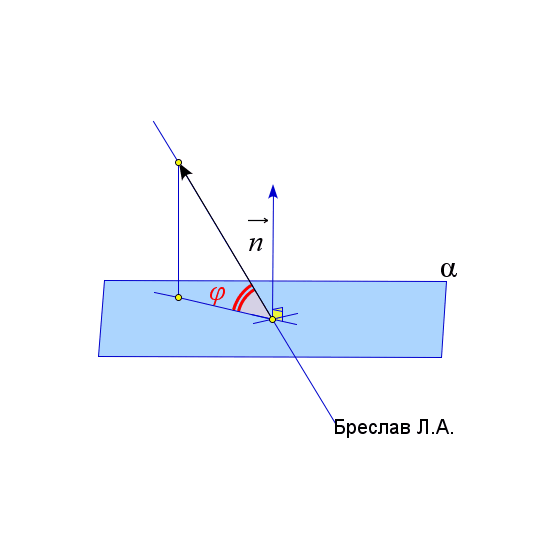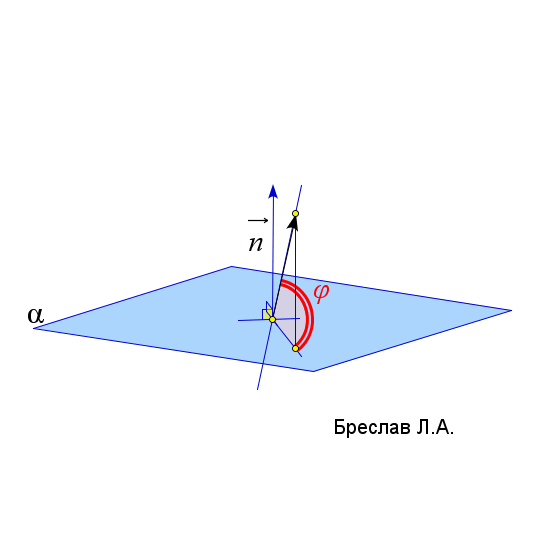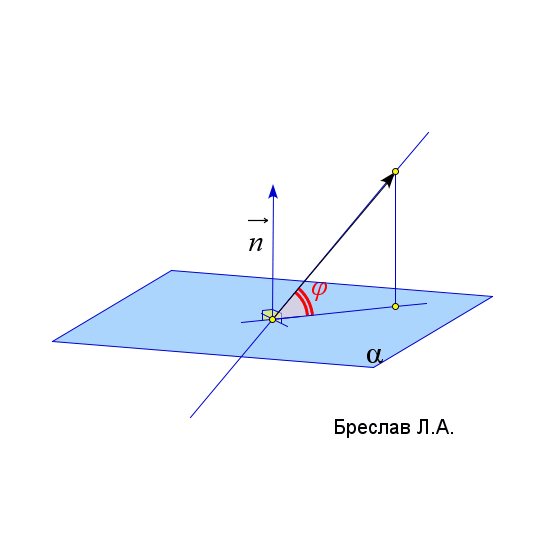
$\vec{a}$ и $\vec{b}$ – направляющие вектора прямых $l_1$ и $l_2$ | $\angle(l;\alpha)=90^\circ-\angle(\vec{a},\vec{n}_\alpha)$
(угол $\angle(\vec{a},\vec{n}_\alpha)$ должен быть острым)
$\vec{a}$ – направляющий вектор прямой $l$
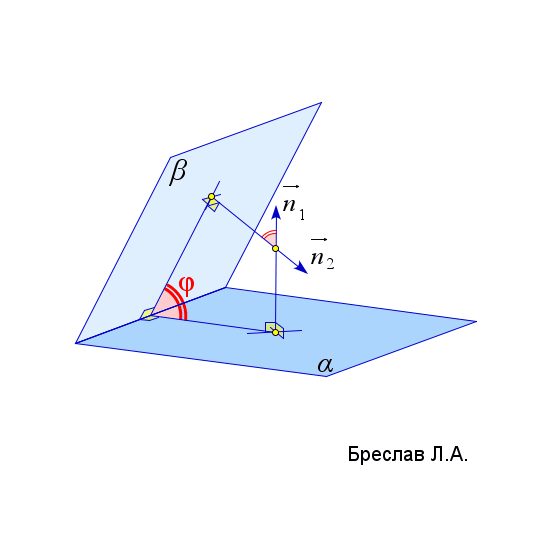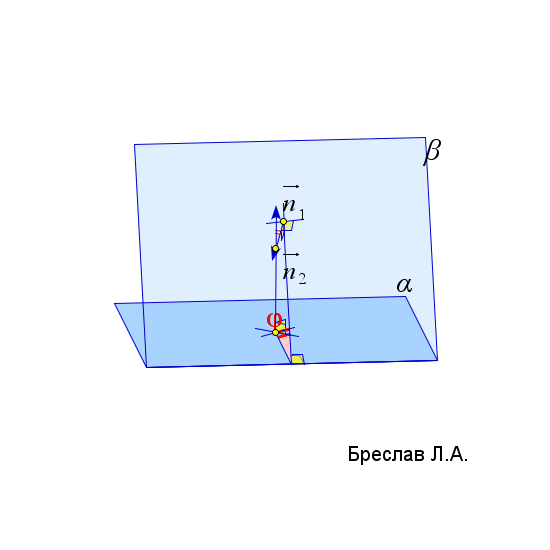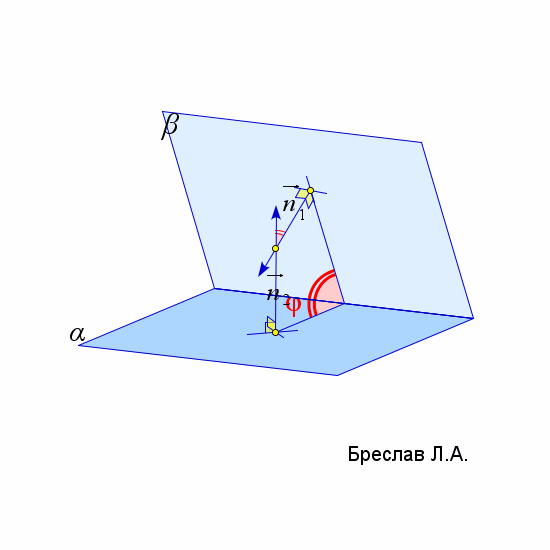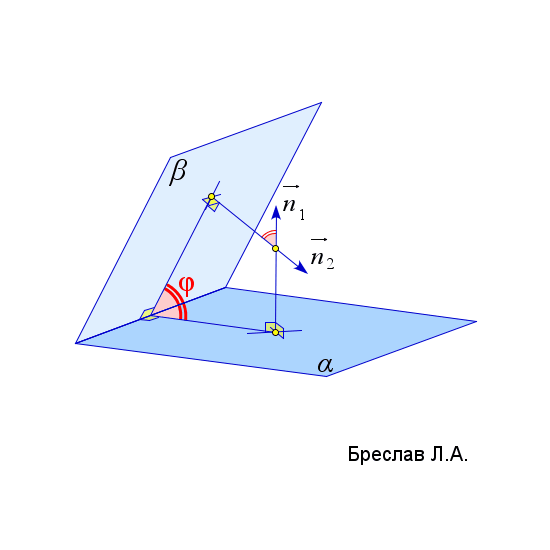
$\vec{n}_\alpha$ – нормаль к плоскости $\alpha$ | $\angle(\alpha;\beta)=\angle(\vec{n}_1;\vec{n}_2)$
(угол $\angle(\vec{n}_1;\vec{n}_2)$ должен быть острым)
$\vec{n}_1$ и $\vec{n}_2$ – нормали к плоскостям $\alpha$ и $\beta$ |
Расстояния и объёмы
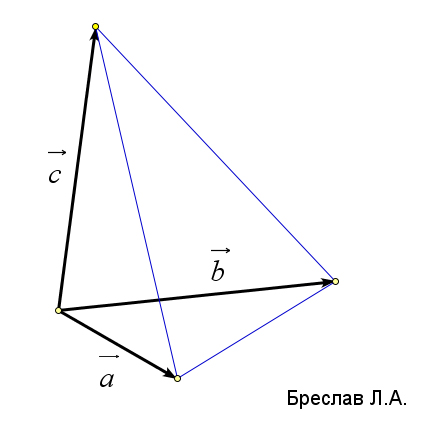
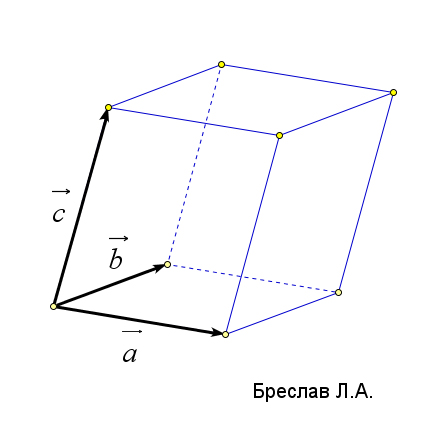
| Расстояние от точки до плоскости | Расстояние между двумя скрещивающимися прямыми | Объём тетраэдра | Объём параллелепипеда |
 |  |  |  |
$\rho(A;\alpha)=\left|\dfrac{(\vec{a},\vec{b},\vec{c})}{|\vec{a}\times\vec{b}|}\right|$
$\vec{a}$ и $\vec{b}$ лежат в плоскости $\alpha$
$\vec{c}$ соединяет точку $A$ и любую точку из плоскости $\alpha$ | $\rho(l_1;l_2)=\left|\dfrac{(\vec{a},\vec{b},\vec{c})}{|\vec{a}\times\vec{b}|}\right|$
$\vec{a}$ и $\vec{b}$ – направляющие вектора прямых
$\vec{c}$ произвольный вектор, соединяющий прямые $l_1$ и $l_2$ | $V=\dfrac{1}{6}\left|(\vec{a}, \vec{b}, \vec{c})\right|$ | $V=\left|(\vec{a}, \vec{b}, \vec{c})\right|$ |
math-public/vectmetodkratko.txt · Последнее изменение: — labreslav