Президентский ФМЛ №239

Два вектора равны тогда и только тогда, когда они сонаправлены и их длины равны.

Таким образом равенство векторов не зависит от выбора системы координат в пространстве. Более того, в разных системах координат равные векторы могут иметь различающиеся координаты, но при этом сами векторы будут равны.

Пусть дана система координат $I$, в которой $(\vec{i},\vec{j},\vec{k})$ – правый базис.

Пусть в данной системе координат $\vec{a}=(x_1;y_1;z_1)$ и $\vec{b}=(x_2;y_2;z_2)$.

Тогда вектор, который получается в результате подсчёта определителя $\left|\begin{array}{ccc}\vec{i}&\vec{j}&\vec{k}\\x_1&y_1&z_1\\x_2&y_2&z_2\end{array}\right|$ обозначим $(\vec{a}\times\vec{b})_{I}$ – векторное произведение векторов $\vec{a}$ и $\vec{b}$ в системе координат $I$.

$$(\vec{a}\times\vec{b})_I = \left|\begin{array}{ccc}\vec{i}&\vec{j}&\vec{k}\\x_1&y_1&z_1\\x_2&y_2&z_2\end{array}\right|=$$ $$ = \vec{i}(y_1z_2-z_1y_2)-\vec{j}(x_1z_2-z_1x_2)+\vec{k}(x_1y_2-y_1x_2)=$$ $$ = (y_1z_2-z_1y_2; -x_1z_2+z_1x_2; x_1y_2-y_1x_2)$$

Так как в разных системах координат вектора $\vec{a}$ и $\vec{b}$ будут иметь разные координаты, то результат векторного умножения $\vec{a}$ на $\vec{b}$ теоретически может зависеть от выбора системы координат. Поэтому используется обозначение $(\vec{a}\times\vec{b})_I$, а не просто $\vec{a}\times\vec{b}$.

Например, в одной системе координат векторное произведение могло дать вектор $\vec{c}_1 = (\vec{a}\times\vec{b})_I$, а во второй системе координат мог получится другой вектор: $\vec{c}_2=(\vec{a}\times\vec{b})_{II}$.

Пусть система координат $II$ получается из системы координат $I$ поворотом вокруг оси $Oz$ на угол $\varphi$.

Пусть $(x_0;y_0;z_0)$ – это координаты точки $A$ в системе координат $I$, а $(\tilde{x};\tilde{y};\tilde{z})$ – координаты точки в системе координат $II$. Тогда верны следующие соотношения: $$\left\{\begin{array}{ll}\tilde{x} = x_0\cos{\varphi}+y\sin{\varphi},\\ \tilde{y} = -x_0\sin{\varphi}+y_0\cos{\varphi},\\\tilde{z} = z_0.\end{array}\right.$$

При повороте системы координат вокруг одной из осей результат векторного произведения не изменяется, как вектор.

Пусть система координат $II$ получается из системы координат $I$ поворотом вокруг оси $Oz$ на угол $\varphi$.

Будем откладывать вектора $\vec{a}$, $\vec{b}$, $(\vec{a}\times\vec{b})_{I}$ и $(\vec{a}\times\vec{b})_{II}$ от начала координат.

Пусть в первой системе координат вектор $\vec{a}$ имеет координаты $(x_1;y_1;z_1)$, а вектор $\vec{b}$ имеет координаты $(x_2;y_2;z_2)$.
Пусть конец вектора $(\vec{a}\times\vec{b})_{I}$ – это точка $C_{1}$. Тогда эта точка $C_{1}$ в первой системе координат имеет координаты $(X_{C_1},Y_{C_1},Z_{C_1}) = (y_1z_2-z_1y_2; -x_1z_2+z_1x_2; x_1y_2-y_1x_2)$.

После поворота системы координат вектор $\vec{a}$ (в новой системе координат) будет иметь координаты $(\tilde{x}_1; \tilde{y}_1; \tilde{z}_1)$.
После поворота системы координат вектор $\vec{b}$ (в новой системе координат) будет иметь координаты $(\tilde{x}_2; \tilde{y}_2; \tilde{z}_2)$.
Пусть конец вектора $(\vec{a}\times\vec{b})_{II}$ – это точка $C_{2}$. Тогда эта точка $C_{2}$ во второй системе координат имеет координаты $(X_{C_2},Y_{C_2},Z_{C_2}) = (\tilde{y}_1\tilde{z}_2-\tilde{z}_1\tilde{y}_2; -\tilde{x}_1\tilde{z}_2+\tilde{z}_1\tilde{x}_2; \tilde{x}_1\tilde{y}_2-\tilde{y}_1\tilde{x}_2)$.

Докажем, что точки $C_{1}$ и $C_{2}$ совпадают. Для этого:

1. найдем координаты точки $C_{1}$ в изначальной системе координат
2. по формулам поворота найдем координаты точки $C_{1}$ в новой системе координат;
3. найдем координаты векторов $\vec{a}$ и $\vec{b}$ в новой системе координат;
4. найдем координаты точки $C_{2}$ в новой системе координат, посчитав $(\vec{a}\times\vec{b})_{II}$;
5. если координаты точки $C_{2}$ совпадут с координатами точки $C_{1}$ (и те, и другие в новой системе координат), то и сами точки совпадают;
6. тогда и векторы $(\vec{a}\times\vec{b})_{I}$ и $(\vec{a}\times\vec{b})_{II}$ будут равны в смысле длины и направления.

Пусть система координат $II$ получается из системы координат $I$ поворотом вокруг оси $Oz$ на угол $\varphi$.

Будем откладывать вектора $\vec{a}$, $\vec{b}$, $(\vec{a}\times\vec{b})_{I}$ и $(\vec{a}\times\vec{b})_{II}$ от начала координат.

Пусть в первой системе координат вектор $\vec{a}$ имеет координаты $(x_1;y_1;z_1)$, а вектор $\vec{b}$ имеет координаты $(x_2;y_2;z_2)$.
Пусть конец вектора $(\vec{a}\times\vec{b})_{I}$ – это точка $C_{1}$. Тогда эта точка $C_{1}$ в первой системе координат имеет координаты $(X,Y,Z) = (y_1z_2-z_1y_2; -x_1z_2+z_1x_2; x_1y_2-y_1x_2)$.

Применяя формулу поворота системы координат, получим, что координаты точки $C_1$ во второй системе координат равны:

$$(X\cdot\cos{\varphi}+Y\cdot\sin{\varphi};\ -X\cdot\sin{\varphi}+Y\cdot\cos{\varphi};\ Z) = $$

$$\Big((y_1z_2-z_1y_2)\cdot\cos{\varphi}+(-x_1z_2+z_1x_2)\cdot\sin{\varphi};\ -(y_1z_2-z_1y_2)\cdot\sin{\varphi}+(-x_1z_2+z_1x_2)\cdot\cos{\varphi};\ x_1y_2-y_1x_2\Big)$$

Во второй системе координат вектор $\vec{a}$ имеет координаты $(x_1\cos{\varphi}+y_1\sin{\varphi};\ -x_1\sin{\varphi}+y_1\cos{\varphi};\ z_1)$.
Во второй системе координат вектор $\vec{b}$ имеет координаты $(x_2\cos{\varphi}+y_2\sin{\varphi};\ -x_2\sin{\varphi}+y_2\cos{\varphi};\ z_2)$.

Вычислим координаты вектора $(\vec{a}\times\vec{b})_{II}$ (это координаты во второй системе координат):

$$(\vec{a}\times\vec{b})_{II}=\left|\begin{array}{ccc}\vec{e_1}&\vec{e_2}&\vec{e_3}\\x_1\cos{\varphi}+y_1\sin{\varphi}&-x_1\sin{\varphi}+y_1\cos{\varphi}&z_1\\ x_2\cos{\varphi}+y_2\sin{\varphi}&-x_2\sin{\varphi}+y_2\cos{\varphi}&z_2\end{array} \right|$$

По новой оси $Ox$:

$$X((\vec{a}\times\vec{b})_{II})=(-x_1\sin{\varphi}+y_1\cos{\varphi})\cdot z_2 - (-x_2\sin{\varphi}+y_2\cos{\varphi})\cdot z_1 =$$ $$ = (-x_1z_2+x_2z_1)\sin{\varphi}+(y_1z_2-y_2z_1)\cos{\varphi}.$$

По новой оси $Oy$:

$$Y((\vec{a}\times\vec{b})_{II})=-(x_1\cos{\varphi}+y_1\sin{\varphi})\cdot z_2 + (x_2\cos{\varphi}+y_2\sin{\varphi})\cdot z_1 = $$ $$ = (-x_1z_2+x_2z_1)\cos{\varphi}+(-y_1z_2+y_2z_1)\sin{\varphi}.$$

По новой оси $Oz$:

$$Z((\vec{a}\times\vec{b})_{II}) = (x_1\cos{\varphi}+y_1\sin{\varphi})(-x_2\sin{\varphi}+y_2\cos{\varphi})- (-x_1\sin{\varphi}+y_1\cos{\varphi})(x_2\cos{\varphi}+y_2\sin{\varphi}) = $$

$$= (-x_1x_2\sin{\varphi}\cos{\varphi}+x_1y_2\cos^2{\varphi}-x_2y_1\sin^2{\varphi}+y_1y_2\sin{\varphi}\cos{\varphi}) -$$

$$ - (-x_1x_2\sin{\varphi}\cos{\varphi}-x_1y_2\sin^2{\varphi}+y_1x_2\cos^2{\varphi}+y_1y_2\sin{\varphi}\cos{\varphi}) = $$

$$ = x_1y_2(\cos^2{\varphi}+\sin^2{\varphi})-x_2y_1(\sin^2{\varphi}+\cos^2{\varphi}) = x_1y_2 - x_2y_1.$$

Таким образом мы нашли координаты точки $C_{2}$ во второй системе координат.

Найденные координаты точки $C_{2}$ совпали с координатами точки $C_1$ в той же, второй, системе координат. Значит и сами точки $C_1$ и $C_2$ совпадают. Значит и вектора $(\vec{a}\times\vec{b})_{I}$ и $(\vec{a}\times\vec{b})_{II}$ равны в смысле длины и направления.

Случаи вращения вокруг осей $Ox$ и $Oy$ доказываются аналогично.

Пусть некомпланарные вектора $\vec{a}, \vec{b}$ и $\vec{c}$ отложены от одной точки. Тогда:

1. Упорядоченная тройка векторов $(\vec{a}, \vec{b}, \vec{c})$ называется правой, если для наблюдателя, находящегося на конце вектора $\vec{c}$, кратчайший поворот вектора $\vec{a}$ к вектору $\vec{b}$ виден против часовой стрелки.
2. Упорядоченная тройка векторов $(\vec{a}, \vec{b}, \vec{c})$ называется левой, если для наблюдателя, находящегося на конце вектора $\vec{c}$, кратчайший поворот вектора $\vec{a}$ к вектору $\vec{b}$ виден по часовой стрелки.

Пусть $(\vec{i},\vec{j},\vec{k})$ – правый базис системы координат. Рассмотрим неколлинеарные вектора $\vec{a}$ и $\vec{b}$. Тогда вектора $(\vec{a}, \vec{b}, \vec{a}\times\vec{b})$ образуют правую тройку векторов.

Ясно, что вектора $\vec{a}$ и $\vec{b}$ можно отложить от начала координат, что не меняет вектор $\vec{a}\times\vec{b}$.

Повернем систему координат так, чтобы вектор $\vec{b}$ был сонаправлен с осью $Oy$, а вектор $\vec{a}$ лежал бы в плоскости $xOy$.

Этого можно добиться тремя последовательными поворотами:

1. Сначала повернем систему координат вокруг оси $Oz$ так, чтобы вектор $\vec{b}$ попал в плоскость новых осей $Oz$ и $Oy$.
2. Затем повернем систему координат вокруг новой оси $Ox$ так, чтобы вектор $\vec{b}$ оказался сонаправлен с осью $Oy$.
3. И, наконец, повернем систему координат вокруг новой оси $Oy$ так, чтобы вектор $\vec{a}$ попал в плоскость новых осей $Ox$ и $Oy$.

При поворотах вокруг осей координат результат векторного произведения не изменяется. Значит, если мы докажем, что в конечной системе координат вектора $\vec{a}, \vec{b}$ и $\vec{a}\times\vec{b}$ образуют правую тройку, то и в изначальной системе координат эти вектора образовывали правую тройку, так как это будут те же самые вектора в смысле длин и направлений.

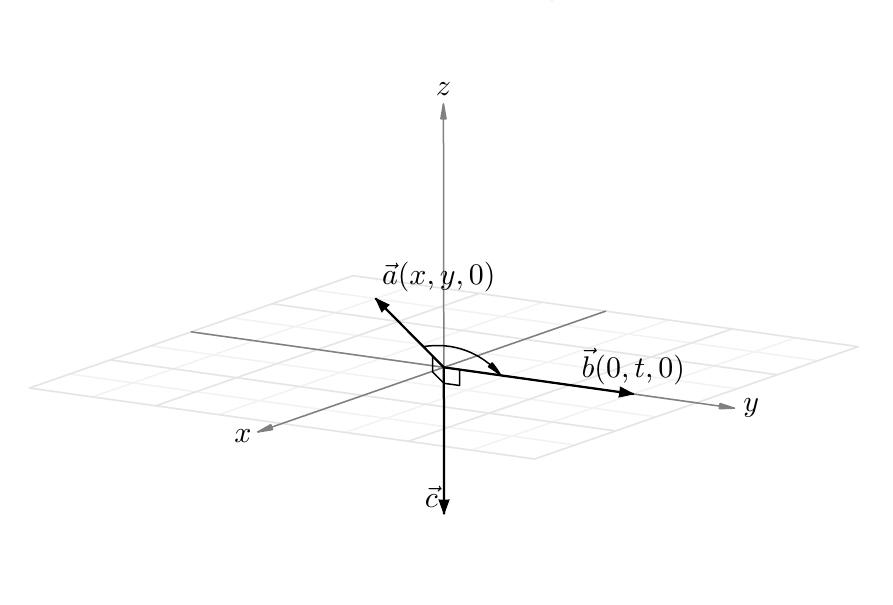
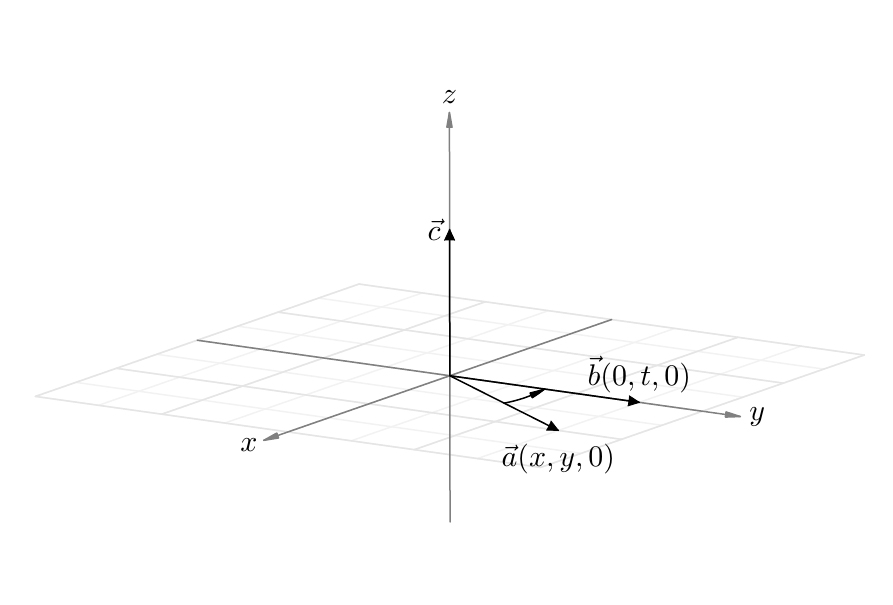
В новой системе координат вектор $\vec{a}$ будет иметь координаты $(x,y,0)$, а вектор $\vec{b}$ будет иметь координаты $(0,t,0)$.

Причем $t\neq 0$, так как $\vec{b}\neq\vec{0}$, и $t>0$, так как вектор $\vec{b}$ сонаправлен с осью $Oy$.

Кроме того $x\neq 0$, так как иначе бы вектора $\vec{a}$ и $\vec{b}$ были бы коллинеарны.

Тогда $\vec{c} = \vec{a}\times\vec{b}=0\cdot\vec{i}+0\cdot\vec{j}+(xt)\cdot\vec{k}=(0,0,xt)$.

Если $x>0$, то $xt>0$, а значит вектор $\vec{c}$ направлен вдоль оси $Oz$ вверх, и тогда видно, что вектора $(\vec{a},\vec{b},\vec{c})$ образуют правую тройку векторов.

Если $x<0$, то $xt<0$, а значит вектор $\vec{c}$ направлен вдоль оси $Oz$ вниз. Но поскольку кратчайшее вращение вектора $\vec{a}$ к вектору $\vec{b}$ теперь происходит в другую сторону, то $(\vec{a},\vec{b},\vec{c})$ снова образуют правую тройку векторов.

Результат векторного произведения, как вектор, не зависит от выбора системы координат, если обе системы координат будут «правыми».

Любые две правые системы координат можно совместить последовательным применением параллельного переноса и трёх поворотов вокруг осей координат.

Но при параллельном переносе системы координат векторное произведение очевидно не изменяется, так как и базис и координаты векторов остаются прежними.

А при поворотах вокруг осей координат векторное произведение не изменяется в силу Теоремы 1.

Таким образом, если использовать только правые системы координат, можно не использовать индексы $I$ или $II$ при обозначении векторного произведения, а писать просто $\vec{a}\times\vec{b}$.