Катет прямоугольного треугольника, лежащий напротив угла в $30^\circ$, равен половине гипотенузы.

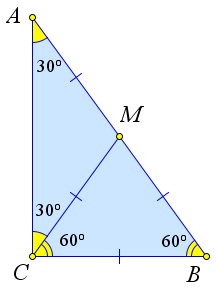
Рассмотрим треугольник $ABC$, в котором $\angle C=90^\circ, \angle A=30^\circ$. Докажем, что $AB=2\cdot CB$.

Пусть $CM$ – медиана.

Тогда $CM=MA=MB$, следовательно, $\triangle AMC$ и $\triangle BMC$ – равнобедренные.

Тогда $\angle A=\angle ACM$, следовательно, $\angle MCB=\angle CBM=60^\circ$.

Тогда $\triangle BCM$ – равносторонний, следовательно, $BC=BM=\frac{1}{2}\cdot AB$.

Если катет прямоугольного треугольника равен половине гипотенузы, то угол, противолежащий этому катету, равен $30^\circ$.

Рассмотрим прямоугольный треугольник $ABC$, в котором $\angle C=90^\circ, BC=\frac{1}{2}\cdot AB$.

Докажем, что $\angle A=30^\circ$.

Проведем медиану $CM$. Тогда по свойству медианы прямоугольного треугольника $CM = AM = BM$.

Тогда треугольник $CMB$ – равносторонний, а, значит $\angle BCM = 60^\circ.$

Тогда $\angle ACM = 30^\circ$.

И поскольку треугольник $ACM$ – равнобедренный, то $\angle A = \angle ACM = 30^\circ.$

Если в треугольнике напротив угла в $30^\circ$ лежит сторона, равная половине другой стороны этого треугольника, то треугольник прямоугольный.

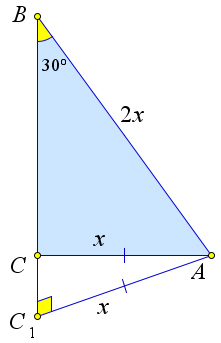
Рассмотрим треугольник $ABC$, в котором $AC=x, AB=2x, \angle B=30^\circ$.

Докажем, что тогда $\angle C=90^\circ$.

Предположим противное, тогда из точки $B$ можно опустить перпендикуляр $AC_1$ на прямую $CB$.

Треугольник $ABC_1$ – прямоугольный,$\angle B=30^\circ$, следовательно, $AC_1=x$.

Тогда $\triangle CAC_1$ – равнобедренный, и $\angle C_1=\angle ACC_1=90^\circ$, что невозможно.

Значит, $\angle C=90^\circ.$

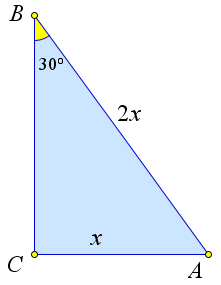
Рассмотрим треугольник $ABC$, в котором $AC=x, AB=2x, \angle B=30^\circ$.

По теореме синусов для $\triangle ABC$: $\dfrac{x}{\sin{30^\circ}}=\dfrac{2x}{\sin{\angle C}}$.

Тогда $\sin{\angle C}=1$, то есть $\angle C=90^\circ$.