Уравнение окружности с центром в точке $O(a;b)$ и радиусом $R$ имеет вид $(x-a)^2+(y-b)^2=R^2$.

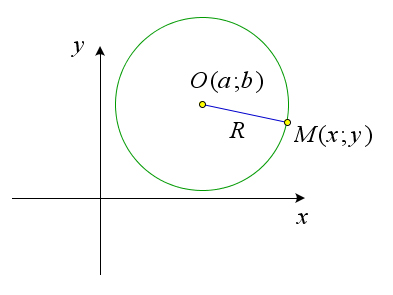
Пусть $M(x;y)$ – это произвольная точка данной окружности.

По определению окружности $OM=R$.

Воспользовавшись формулой расстояния между двумя точками, получим $\sqrt{(x-a)^2+(y-b)^2}=R$ или $(x-a)^2+(y-b)^2=R^2$.