Президентский ФМЛ №239

Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции.

Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме.

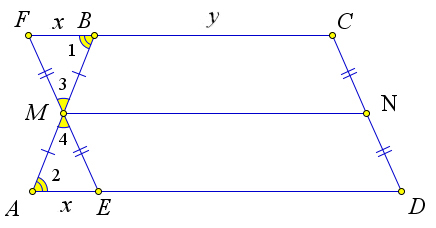
Рассмотрим трапецию $ABCD$, в которой проведена средняя линия $MN$.

Докажем, что $MN\parallel AD$ и $MN=\frac{AD+BC}{2}$.

Проведем через точку $M$ прямую $FE$ параллельно $CD$ ($F\in CB, E\in AD$).

Тогда $FCDE$ – параллелограмм ($FC\parallel ED, FE\parallel CD$).

Следовательно, $FE=CD$, $FC=ED$.

Кроме того $\triangle FBM=\triangle AME$, по второму признаку равенства ($\angle 1=\angle 2$, как накрест лежащие, $\angle 3=\angle 4$, как вертикальные, $AM=MB$, так как $M$ – середина).

Следовательно, $FM=ME$.

Тогда $FMNC$ и $MNDE$ - параллелограммы ($FM=ME=ND=NC$ и $FE\parallel CD$).

Следовательно, $MN\parallel BC$.

Кроме того, из равенства треугольников $\triangle FBM=\triangle AME$ следует,что $FB=AE$.

Пусть $FB=AE=x$ и $BC=y$.

Тогда $FC=ED=x+y$.

Следовательно, $MN=x+y$.

Кроме того, $BC+AD=BC+AE+ED=y+x+(x+y)=2x+2y$.

Таким образом, $MN=x+y=\dfrac{BC+AD}{2}$.

1. Пусть отрезок $MN$ соединяет точки на боковых сторонах трапеции. Если $M$ – середина боковой стороны, и $MN$ параллелен основаниям трапеции, то $MN$ – это средняя линия трапеции.
2. Пусть отрезок $MN$ соединяет точки на боковых сторонах трапеции. Если $MN$ параллелен основанием трапеции и равен их полусумме, то $MN$ – средняя линия трапеции.

Первый пункт теоремы является прямым следствием теоремы Фалеса.

Докажем второй пункт теоремы.

Рассмотрим трапецию $ABCD$, в которой на боковых сторонах $AB$ и $CD$ выбраны точки $M$ и $N$ соответственно, и при этом $MN=\dfrac{AD+BC}{2}$.

Докажем, что тогда $MN$ – средняя линия трапеции $ABCD$.

Предположим противное, то есть $MN$ – не средняя линия данной трапеции.

Если ровно одна из точек $M$ или $N$ является серединой, то по первому пункту теоремы $MN$ – это средняя линия, так как $MN$ параллельна основаниям трапеции.

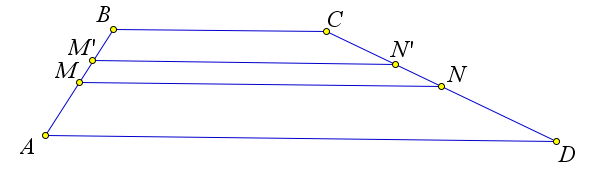
Пусть точки $M$ и $N$ – не середины боковых сторон.

Тогда пусть $M'N'$ – средняя линия трапеции.

Следовательно, $M'N'=\frac{BC+AD}{2}=MN$ и $MN\parallel BC\parallel MN$.

Но тогда $MNN'M'$ – параллелограмм, и, следовательно, $MM'\parallel NN'$, что противоречит тому, что $ABCD$ – это трапеция.

Следовательно, $MN$ – средняя линия.

Отрезок, соединяющий середины диагоналей трапеции, равен полуразности ее оснований.

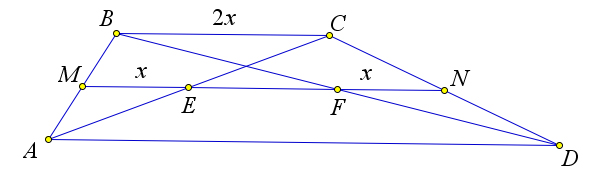
Рассмотрим трапецию $ABCD$, в которой точки $E$ и $F$ – это середины диагоналей $AC$ и $BD$ соответственно.

Докажем, что $EF=\frac{AD-BC}{2}$.

По теореме Фалеса средняя линия трапеции $MN$ делит диагонали $AC$ и $BD$ пополам, то есть точки $E$ и $F$ лежат на средней линии.

Тогда $ME$ и $FN$ – это средние линии треугольников $\triangle ABC$ и $\triangle DBC$.

Следовательно, если обозначить $BC=2x$, то $ME=FN=x$.

Тогда $EF=\frac{2x+AD}{2}-x-x=\frac{AD-2x}{2}=\frac{AD-BC}{2}$.